
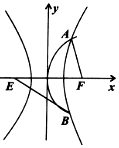
 已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于不同的两点A,B,若$|AF|=\frac{4}{5}|BE|$,则双曲线的离心率为$4±\sqrt{7}$.
已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于不同的两点A,B,若$|AF|=\frac{4}{5}|BE|$,则双曲线的离心率为$4±\sqrt{7}$. 分析 根据双曲线的定义求出|BE|=10a,|BF|=8a,结合抛物线的定义求出交点B的纵坐标,结合直角三角形的边角关系建立方程进行求解即可.
解答 解:根据双曲线和抛物线的对称性得|BF|=|AF|=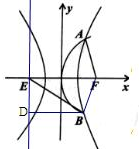 $\frac{4}{5}$|BE|,
$\frac{4}{5}$|BE|,
∵|BE|-|BF|=2a,
∴|BE|-$\frac{4}{5}$|BE|=$\frac{1}{5}$|BE|=2a,
则|BE|=10a,|BF|=8a,
∵抛物线y2=2px(p>0)与双曲线有公共的焦点F,
∴$\frac{p}{2}$=c,且x=-c是抛物线的准线,
则|BD|=|BF|=8a,
设B(x,y),则由抛物线的性质得x+c=8a,即x=8a-c,
代入抛物线方程y2=2px=4cx得y2=4c(8a-c),
则|DE|2=y2=4c(8a-c),
在直角三角形BDE中,
BE2=DE2+BD2,
即100a2=64a2+4c(8a-c),
即36a2-32ac+4c2=0,
即c2-8ac+9a2=0,
解e2-8e+9=0,
得e=$4±\sqrt{7}$,
故答案为$4±\sqrt{7}$.
点评 本题主要考查双曲线离心率的计算,根据抛物线和双曲线的定义建立方程关系,求出a,c的关系是解决本题的关键.综合性较强,有一定的难度.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lnx≥x+1 | B. | lnx≤1-x | C. | lnx≥x-1 | D. | lnx≤x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$-3 | B. | $\sqrt{5}$-2 | C. | 3-$\sqrt{5}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 导师转身人数(人) | 4 | 3 | 2 | 1 |
| 获得相应导师转身的选手人数(人) | 1 | 2 | 2 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com