
【题目】《九章算术》是我国古代的数学名著,书中把三角形的田称为“圭田”,把直角梯形的田称为“邪田”,称底是“广”,称高是“正从”,“步”是丈量土地的单位.现有一邪田,广分别为十步和二十步,正从为十步,其内有一块广为八步,正从为五步的圭田.若在邪田内随机种植一株茶树,求该株茶树恰好种在圭田内的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() 的左、右焦点,
的左、右焦点,![]() 恰好与抛物线
恰好与抛物线![]() 的焦点重合,过椭圆
的焦点重合,过椭圆![]() 的左焦点
的左焦点![]() 且与
且与![]() 轴垂直的直线被椭圆
轴垂直的直线被椭圆![]() 截得的线段长为3.
截得的线段长为3.
(1)求椭圆![]() 的方程;
的方程;
(2)已知点![]() ,直线
,直线![]() :
:![]() ,过
,过![]() 斜率为
斜率为![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 交于
交于![]() 点,若直线
点,若直线![]() ,
,![]() ,
,![]() 的斜率分别是
的斜率分别是![]() ,
,![]() ,
,![]() ,求证:无论
,求证:无论![]() 取何值,总满足
取何值,总满足![]() 是
是![]() 和
和![]() 的等差中项.
的等差中项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A4纸是生活中最常用的纸规格.A系列的纸张规格特色在于:①A0、A1、A2…、A5,所有尺寸的纸张长宽比都相同.②在A系列纸中,前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张A0纸对裁后可以得到2张A1纸,1张A1纸对裁可以得到2张A2纸,依此类推.这是因为A系列纸张的长宽比为![]() :1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈
:1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈![]() ,那么A4纸的长度为( )
,那么A4纸的长度为( )
A.![]() 厘米B.
厘米B.![]() 厘米C.
厘米C.![]() 厘米D.
厘米D.![]() 厘米
厘米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),圆
为参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于
交于![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),g(x)分别由下表给出,


则f[g(1)]的值为________,满足f[g(x)]>g[f(x)]的x的值是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用![]() 表示学生掌握和接收概念的能力(
表示学生掌握和接收概念的能力(![]() 的值越大,表示接受能力越强),
的值越大,表示接受能力越强),![]() 表示提出和讲授概念的时间(单位:分钟),可以有以下公式:
表示提出和讲授概念的时间(单位:分钟),可以有以下公式: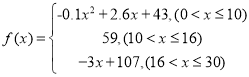
(1)开讲多少分钟后,学生的接受能力最强?能维持多长时间?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com