
【题目】设m∈R,函数f(x)=ex﹣m(x+1) ![]() m2(其中e为自然对数的底数)
m2(其中e为自然对数的底数)
(Ⅰ)若m=2,求函数f(x)的单调递增区间;
(Ⅱ)已知实数x1 , x2满足x1+x2=1,对任意的m<0,不等式f(x1)+f(0)>f(x2)+f(1)恒成立,求x1的取值范围;
(Ⅲ)若函数f(x)有一个极小值点为x0 , 求证f(x0)>﹣3,(参考数据ln6≈1.79)
【答案】解:(Ⅰ)m=2时,f(x)=ex﹣2x﹣1,f′(x)=ex﹣2,
令f′(x)>0,解得:x>ln2,
故函数f(x)在[ln2,+∞)递增;
(Ⅱ)∵不等式f(x1)+f(0)>f(x2)+f(1)恒成立,x1+x2=1,
∴2(x1﹣1)m﹣( ![]() ﹣
﹣ ![]() )+e﹣1<0对任意m<0恒成立,
)+e﹣1<0对任意m<0恒成立,
令g(m)=2(x1﹣1)m﹣( ![]() ﹣
﹣ ![]() )+e﹣1,
)+e﹣1,
当2(x1﹣1)=0时,g(m)=0<0不成立,
则 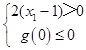 ,解得:x1>1;
,解得:x1>1;
(Ⅲ)由题意得f′(x)=ex﹣m,f′(x0)=0,故 ![]() =m,
=m,
f(x0)= ![]() ﹣m(x0+1)+
﹣m(x0+1)+ ![]() m2=
m2= ![]() m2﹣mlnm,m>0,
m2﹣mlnm,m>0,
记h(m)= ![]() m2﹣mlnm,m>0,
m2﹣mlnm,m>0,
h′(m)= ![]() m﹣lnm﹣1,h′′(m)=
m﹣lnm﹣1,h′′(m)= ![]() ﹣
﹣ ![]() ,
,
当0<m<2时,h′′(m)<0,当m>2时,h′′(m)>0,
故函数h′(x)在(0,2)递减,在(2,+∞)递增,
如图所示:
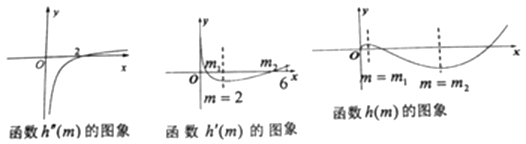
[h′(m)]min=h′(2)=﹣ln2<0,
又当m→0时,h′(m)>0,m→+∞,h′(m)>0,
故函数h′(m)=0有2个根,记为m1,m2(m1<2<m2<6),(h′(6)>0),
故h(m)在(0,m1)递增,在(m1,m2)递减,在(m2,+∞)递增,
又当m→0时,h(m)>0,h(m)在m2处取极小值,
由h′(m2)=0, ![]() m2﹣lnm2﹣1=0,lnm2=
m2﹣lnm2﹣1=0,lnm2= ![]() m2﹣1,
m2﹣1,
故h(m2)= ![]() ﹣m2lnm2=
﹣m2lnm2= ![]() ﹣m2(
﹣m2( ![]() m2﹣1)
m2﹣1)
=﹣ ![]() +m2=﹣
+m2=﹣ ![]() +1∈(﹣3,1),
+1∈(﹣3,1),
故f(x0)>﹣3
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的递增区间即可;(Ⅱ)问题转化为2(x1﹣1)m﹣( ![]() ﹣
﹣ ![]() )+e﹣1<0对任意m<0恒成立,令g(m)=2(x1﹣1)m﹣(
)+e﹣1<0对任意m<0恒成立,令g(m)=2(x1﹣1)m﹣( ![]() ﹣
﹣ ![]() )+e﹣1,得到关于x1的不等式组,解出即可;(Ⅲ)求出f(x0)的解析式,记h(m)=
)+e﹣1,得到关于x1的不等式组,解出即可;(Ⅲ)求出f(x0)的解析式,记h(m)= ![]() m2﹣mlnm,m>0,根据函数的单调性求出h(m)的取值范围,从而求出f(x0)的范围,证明结论即可.
m2﹣mlnm,m>0,根据函数的单调性求出h(m)的取值范围,从而求出f(x0)的范围,证明结论即可.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】三人独立破译同一份密码.已知三人各自破译出密码的概率分别为 ![]() ,且他们是否破译出密码互不影响. (Ⅰ)求恰有二人破译出密码的概率;
,且他们是否破译出密码互不影响. (Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
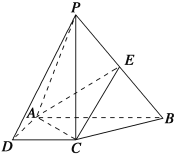
(1)求证:平面EAC⊥平面PBC;
(2)若二面角P-AC-E的余弦值为![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=x﹣ln x﹣2.
(Ⅰ)求函数 f ( x)的最小值;
(Ⅱ)如果不等式 x ln x+(1﹣k)x+k>0(k∈Z)在区间(1,+∞)上恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在12件同类型的零件中有2件次品,抽取3次进行检验,每次抽取1件,并且取出后不再放回,若以ξ和η分别表示取到的次品数和正品数.
(1)求ξ的分布列、均值和方差;
(2)求η的分布列、均值和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=![]() ,其中2<m<2,m∈Z,满足:
,其中2<m<2,m∈Z,满足:
(1)f(x)是区间(0,+∞)上的增函数;
(2)对任意的x∈R,都有f(x) +f(x)=0.
求同时满足条件(1)、(2)的幂函数f(x)的解析式,并求x∈[0,3]时,f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M、N分别是AB、PC的中点.

(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在区间(﹣2,a)(a>0)上任取一个数m,若函数f(x)=3x+m﹣3 ![]() 在区间[1,+∞)无零点的概率不小于
在区间[1,+∞)无零点的概率不小于 ![]() ,则实数a能取的最小整数是( )
,则实数a能取的最小整数是( )
A.1
B.3
C.5
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com