【题目】如图，在四棱锥
中，底面ABCD为梯形，AB//CD，
，AB=AD=2CD=2，△ADP为等边三角形．
(1)当PB长为多少时，平面
平面ABCD?并说明理由；
(2)若二面角
大小为150°，求直线AB与平面PBC所成角的正弦值．
【答案】（1）当
时，平面
平面
，详见解析（2）
【解析】
(1)根据平面和平面垂直可得线面垂直，从而可得
,利用直角三角形知识可得
的长；
(2)构建空间直角坐标系，利用法向量求解直线AB与平面PBC所成角的正弦值.
解：（1）当时，平面平面，
证明如下：在
中，因为
，所以，
又
，
，所以
平面
，
又
平面，所以平面平面；
（2）分别取线段
的中点
，连接
，因为
为等边三角形，
为
的中点，所以
，为的中点，所以
,
又，所以
，故
为二面角
的平面角，所以
，
如图，分别以
的方向以及垂直于平面向上的方向作为
轴的正方向，建立空间直角坐标系
，
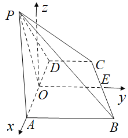
因为
，，所以
，
，
，
.
可得
，
，
设
为平面
的一个法向量，则有
，
即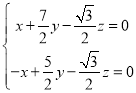
，令
，
可得
，
设
与平面所成角为
，则有
所以直线与平面所成角的正弦值为.
科目：高中数学 来源： 题型：
【题目】在2018、2019每高考数学全国Ⅰ卷中，第22题考查坐标系和参数方程，第23题考查不等式选讲.2018年髙考结束后，某校经统计发现:选择第22题的考生较多并且得分率也较高.为研究2019年选做题得分情况，该校高三质量检测的命题完全采用2019年高考选做题模式，在测试结束后，该校数学教师对全校高三学生的选做题得分进行抽样统计，得到两题得分的统计表如下(已知每名学生只选做—道题):
第22题的得分统计表
得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 50 | 50 | 75 | 125 | 200 |
文科人数 | 25 | 25 | 125 | 0 | 25 |
第23题的得分统计表
得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 30 | 52 | 58 | 60 | 200 |
文科人数 | 5 | 10 | 10 | 5 | 70 |
(1)完成如下2×2列联表，并判断能否有99%的把握认为“选做题的选择”与“文、理科的科类”有关；
选做22题 | 选做23题 | 总计 | |
理科人数 | |||
文科人数 | |||
总计 |
(2)若以全体高三学生选题的平均得分作为决策依据，如果你是考生，根据上面统计数据，你会选做哪道题，并说明理由.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着移动互联网的快速发展，基于互联网的共享单车应运而生．某市场研究人员为了了解共享单车运营公司
的经营状况，对该公司最近六个月（2017年5月到2017年10月）内在西安市的市场占有率进行了统计，并绘制了相应的折线图．
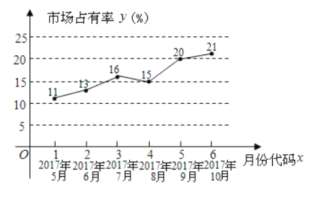
（1）由拆线图可以看出，可用线性回归模型拟合月度市场占有率
与月份代码
之间的关系．求关于的线性回归方程；
（2）公司对员工承诺如果公司的共享单车在2017年年底（12月底）能达到西安市场占有率的
，员工每人都可以获得年终奖，依据上面计算得到回归方程估计员工是否能得到年终奖．
（参考公式：回归直线方程为
，其中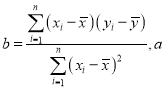
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于数列
，如果存在正整数
，使得
对一切
，
都成立，则称数列为
等差数列．
（1）若数列为2-等差数列，且前四项分别为2，-1，4，-3，求
的值；
（2）若既是2-等差数列，又是3-等差数列，证明：是等差数列．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】[选修4—4：坐标系与参数方程]:在直角坐标系
中，直线
的参数方程为
（t为参数，
），以坐标原点为极点，以x轴的非负半轴为极轴，建立极坐标系，曲线C的极坐标方程为
，已知直线与曲线C交于不同的两点A，B．
(1)求直线的普通方程和曲线C的直角坐标方程；
(2)设P(1，2)，求
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知圆
的方程为
，
点的坐标为
.
（1）求过点且与圆相切的直线方程；
（2）过点任作一条直线
与圆交于不同两点
，
，且圆交
轴正半轴于点
，求证：直线
与
的斜率之和为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱柱ABCD－A1B1C1D1中，侧棱AA1⊥底面ABCD，AB∥DC，
．
（Ⅰ）求证：CD⊥平面ADD1A1；
（Ⅱ）若直线AA1与平面AB1C所成角的正弦值为
，求k的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，直线
的参数方程为
为参数），以
为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
，点
是曲线上的动点，点
在
的延长线上，且
，点的轨迹为
．
（1）求直线及曲线的极坐标方程；
（2）若射线
与直线交于点
，与曲线交于点
（与原点不重合），求
的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在三棱锥P﹣ABC中，D为AB的中点．
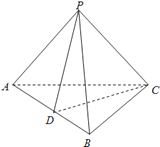
（1）与BC平行的平面PDE交AC于点E，判断点E在AC上的位置并说明理由如下：
（2）若PA=PB，且△PCD为锐角三角形，又平面PCD⊥平面ABC，求证：AB⊥PC．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
