
 中,每行中的三个数成等差数列,且a11+a12+a13、a21+a22+a23、a31+a32+a33成等比数列,下列四个判断正确的有( )
中,每行中的三个数成等差数列,且a11+a12+a13、a21+a22+a23、a31+a32+a33成等比数列,下列四个判断正确的有( )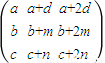 ,由a11+a12+a13,a21+a22+a23,a31+a32+a33成等比数列,则有:(b+m)2=(a+d)(c+n),得出①正确;再由(a+d)+(c+n)≥2
,由a11+a12+a13,a21+a22+a23,a31+a32+a33成等比数列,则有:(b+m)2=(a+d)(c+n),得出①正确;再由(a+d)+(c+n)≥2  =2(b+m),得到③④正确;再根据题设列举出由9个正数组成的特殊矩阵判断②正确即可.
=2(b+m),得到③④正确;再根据题设列举出由9个正数组成的特殊矩阵判断②正确即可. ,由a11+a12+a13,a21+a22+a23,a31+a32+a33成等比数列
,由a11+a12+a13,a21+a22+a23,a31+a32+a33成等比数列 =2(b+m),故③正确;
=2(b+m),故③正确; ,故②正确;
,故②正确;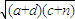 =3-2(b+m),
=3-2(b+m),

科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市徐汇区高三第一学期学习能力诊断卷理科数学 题型:选择题
由9个互不相等的正数组成的矩阵 中,每行中的三个数成等差数列,且
中,每行中的三个数成等差数列,且 、
、 、
、 成等比数列,下列四个判断正确的有……………………( )
成等比数列,下列四个判断正确的有……………………( )
①第2列 必成等比数列
②第1列
必成等比数列
②第1列 不一定成等比数列
不一定成等比数列
③ ④若9个数之和等于9,则
④若9个数之和等于9,则
(A)4个 (B)3个 (C)2个 (D)1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com