
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
, ![]() ,过
,过![]() 与坐标轴不垂直的直线
与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() ,
, ![]() 的中点为
的中点为![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求实数
?若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有250人参与学习先修课程.
(Ⅰ)这两年学校共培养出优等生150人,根据下图等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过0.01的前提下认为学习先修课程与优等生有关系?

优等生 | 非优等生 | 总计 | |
学习大学先修课程 | 250 | ||
没有学习大学先修课程 | |||
总计 | 150 |
(Ⅱ)某班有5名优等生,其中有2名参加了大学生先修课程的学习,在这5名优等生中任选3人进行测试,求这3人中至少有1名参加了大学先修课程学习的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 ,(
,(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程和圆
的极坐标方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为圆
为圆![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F且EF=![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
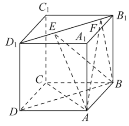
A.AC⊥BEB.EF![]() 平面ABCD
平面ABCD
C.三棱锥A-BEF的体积为定值D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种汽车,购车费用是10万元,第一年维修费用是0.2万元,以后逐年递增0.2万元,且每年的保险费、养路费、汽油费等约为0.9万元.
(1)设这种汽车使用![]() 年(
年(![]() )的维修费用的和为
)的维修费用的和为![]() 万元,求
万元,求![]() 的表达式;
的表达式;
(2)这种汽车使用多少年时,它的年平均费用最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
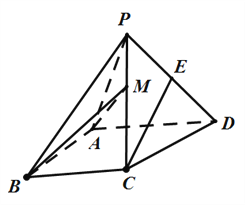
【题目】如图,四棱锥P-ABCD中,侧面PAD是边长为2的等边三角形且垂直于底![]() ,
, ![]()
![]() 是
是![]() 的中点。
的中点。
(1)证明:直线![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】针对时下的“抖音热”,某校团委对“学生性别和喜欢抖音是否有关”作了一次调查,其中被调查的女生人数是男生人数的![]() ,男生喜欢抖音的人数占男生人数的
,男生喜欢抖音的人数占男生人数的![]() ,女生喜欢抖音的人数占女生人数
,女生喜欢抖音的人数占女生人数![]() 若有95%的把握认为是否喜欢抖音和性别有关,则男生至少有( )人.
若有95%的把握认为是否喜欢抖音和性别有关,则男生至少有( )人.
(K2≥k0) | 0.050 | 0.010 |
k0 | 3.841 | 6.635 |
A. 12B. 6C. 10D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知点A(5,-2),B(7,3),且边AC的中点M在y轴上,边BC的中点N在x轴上,求:
(1)顶点C的坐标;
(2)直线MN的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com