
【题目】已知函数![]() .
.
(1)若函数![]() 存在不小于
存在不小于![]() 的极小值,求实数
的极小值,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,若对
时,若对![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用导数分析函数![]() 的单调性,求出函数
的单调性,求出函数![]() 的极值,然后令极值大于等于
的极值,然后令极值大于等于![]() ,解出不等式可得出实数
,解出不等式可得出实数![]() 的取值范围;
的取值范围;
(2)构造函数![]() ,问题等价于
,问题等价于![]() ,对实数
,对实数![]() 进行分类讨论,分析函数
进行分类讨论,分析函数![]() 在区间
在区间![]() 上的单调性,结合条件
上的单调性,结合条件![]() 可得出实数
可得出实数![]() 的取值范围.
的取值范围.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
此时,函数![]() 无极值;
无极值;
当![]() 时,令
时,令![]() ,得
,得![]() ,
,
又当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,函数![]() 在
在![]() 时取得极小值,且极小值为
时取得极小值,且极小值为![]() .
.
令![]() ,即
,即![]() ,得
,得![]() .
.
综上所述,实数![]() 的取值范围为
的取值范围为![]() ;
;
(2)当![]() 时,问题等价于
时,问题等价于![]() ,
,
记![]() ,
,
由(1)知,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() ,
,
①当![]() 时,由
时,由![]() 可知,所以
可知,所以![]() 成立;
成立;
②当![]() 时,
时,![]() 的导函数为
的导函数为![]() 恒成立,所以
恒成立,所以![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() .
.
所以,函数![]() 在区间
在区间![]() 上单调递增,从而
上单调递增,从而![]() ,命题成立.
,命题成立.
③当![]() 时,显然
时,显然![]() 在区间
在区间![]() 上单调递增,
上单调递增,
记![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,
,
所以,函数![]() 在区间
在区间![]() 上为增函数,即当
上为增函数,即当![]() 时,
时,![]() .
.
![]() ,
,![]() ,
,
所以在区间![]() 内,存在唯一的
内,存在唯一的![]() ,使得
,使得![]() ,
,
且当![]() 时,
时,![]() ,即当
,即当![]() 时,
时,![]() ,不符合题意,舍去.
,不符合题意,舍去.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
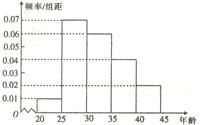
(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天气预报说,在今后的三天中,每天下雨的概率都为![]() .现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:用
.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:用![]() 表示下雨,从下列随机数表的第
表示下雨,从下列随机数表的第![]() 行第
行第![]() 列的
列的![]() 开始读取,直到读取了
开始读取,直到读取了![]() 组数据,
组数据,
18 18 07 92 45 44 17 16 58 09 79 83 86 19 62 06 76 50 03 10
55 23 64 05 05 26 62 38 97 75 34 16 07 44 99 83 11 46 32 24
据此估计,这三天中恰有两天下雨的概率近似为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某刻考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差![]() (单位:分)与物理偏差
(单位:分)与物理偏差![]() (单位:分)之间的关系进行偏差分析,决定从全班40位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如表:
(单位:分)之间的关系进行偏差分析,决定从全班40位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如表:

(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若这次考试该班数学平均分为120分,物理平均分为92,试预测数学成绩126分的同学的物理成绩.
参考公式:  ,
, ![]()
参考数据: ![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,C、D是以AB为直径的圆上两点,AB=2AD=2![]() ,AC=BC,F 是AB上一点,且AF=
,AC=BC,F 是AB上一点,且AF=![]() AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知CE=
AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知CE=![]() .
.

(1)求证:AD⊥平面BCE;
(2)求证:AD∥平面CEF;
(3)求三棱锥A﹣CFD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】写出下列命题的否定,并判断所得命题的真假:
(1)二次函数![]() 的图像的顶点坐标是
的图像的顶点坐标是![]() ;
;
(2)正数的立方根都是正数;
(3)存在一个最大的内角小于60°的三角形;
(4)对任意实数t,点![]() 都在一次函数
都在一次函数![]() 的图像上.
的图像上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com