
【题目】甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为 ![]() ,乙获胜的概率为
,乙获胜的概率为 ![]() ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)记X为比赛决胜出胜负时的总局数,求X的分布列和均值(数学期望).
【答案】
(1)解:用A表示甲在4局以内(含4局)赢得比赛的是事件,Ak表示第k局甲获胜,Bk表示第k局乙获胜,
则P(Ak)= ![]() ,P(Bk)=
,P(Bk)= ![]() ,k=1,2,3,4,5
,k=1,2,3,4,5
P(A)=P(A1A2)+P(B1A2A3)+P(A1B2A3A4)=( ![]() )2+
)2+ ![]() ×(
×( ![]() )2+
)2+ ![]() ×
× ![]() ×(
×( ![]() )2=
)2= ![]() .
.
(2)解:X的可能取值为2,3,4,5.
P(X=2)=P(A1A2)+P(B1B2)= ![]() ,
,
P(X=3)=P(B1A2A3)+P(A1B2B3)= ![]() ,
,
P(X=4)=P(A1B2A3A4)+P(B1A2B3B4)= ![]() ,
,
P(X=5)=P(A1B2A3B4A5)+P(B1A2B3A4B5)+P(B1A2B3A4A5)+P(A1B2A3B4B5)= ![]() =
= ![]() ,
,
或者P(X=5)=1﹣P(X=2)﹣P(X=3)﹣P(X=4)= ![]() ,
,
故分布列为:
X | 2 | 3 | 4 | 5 |
P |
|
|
|
E(X)=2× ![]() +3×
+3× ![]() +4×
+4× ![]() +5×
+5× ![]() =
= ![]() .
.
【解析】(1)根据概率的乘法公式,求出对应的概率,即可得到结论.(2)利用离散型随机变量分别求出对应的概率,即可求X的分布列;以及均值.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 分别为
分别为![]() 的三内角A,B,C的对边,其面积
的三内角A,B,C的对边,其面积![]() ,在等差数列
,在等差数列![]() 中,
中,![]() ,公差
,公差![]() .数列
.数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是两个不同的平面,
是两个不同的平面,![]() 是两条不同的直线,有如下四个命题:
是两条不同的直线,有如下四个命题:
①若![]() ,则
,则![]() ; ②若
; ②若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() ; ④若
; ④若![]() ,则
,则![]() .
.
其中真命题为_________(填所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1 , F2分别是椭圆E:x2+ ![]() =1(0<b<1)的左、右焦点,过点F1的直线交椭圆E于A、B两点,若|AF1|=3|F1B|,AF2⊥x轴,则椭圆E的方程为 .
=1(0<b<1)的左、右焦点,过点F1的直线交椭圆E于A、B两点,若|AF1|=3|F1B|,AF2⊥x轴,则椭圆E的方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如右图所示.经销商为下一个销售季度购进了130t该农产品.以![]() (单位:t,100≤
(单位:t,100≤![]() ≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.

(Ⅰ)将T表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润T不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2 , l1与E1 , E2分别交于A1、A2两点,l2与E1、E2分别交于B1、B2两点. 
(1)证明:A1B1∥A2B2;
(2)过O作直线l(异于l1 , l2)与E1、E2分别交于C1、C2两点.记△A1B1C1与△A2B2C2的面积分别为S1与S2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(![]() )(A>0,ω>0,
)(A>0,ω>0,![]() )的部分图象如图所示.若横坐标分别为-1、1、5的三点M,N,P都在函数f(x)的图象上,则sin∠MNP的值为( )
)的部分图象如图所示.若横坐标分别为-1、1、5的三点M,N,P都在函数f(x)的图象上,则sin∠MNP的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对所有高校学生进行普通话水平测试,发现成绩服从正态分布N(μ,σ2),下表用茎叶图列举出来抽样出的10名学生的成绩.
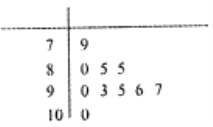
(1)计算这10名学生的成绩的均值和方差;
(2)给出正态分布的数据:P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544.
由(1)估计从全市随机抽取一名学生的成绩在(76,97)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com