
【题目】如图1,在边长为![]() 的正方形中
的正方形中![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,沿
的中点,沿![]() 将矩形
将矩形![]() 折起使得
折起使得![]() ,如图2所示,点
,如图2所示,点![]() 在
在![]() 上,
上,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点.
中点.
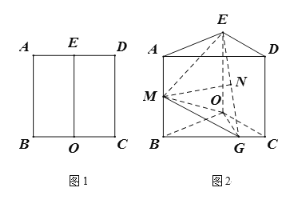
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)取![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() ,利用中位线可得
,利用中位线可得![]() 且
且![]() ,由直棱锥性质可知
,由直棱锥性质可知![]() 且
且![]() ,即可证得四边形
,即可证得四边形![]() 是平行四边形,进而
是平行四边形,进而![]() ,再由线面平行的判定定理说明即可;
,再由线面平行的判定定理说明即可;
(2)由余弦定理,已知以及勾股定理可说明![]() ,易证
,易证![]() ,由线面垂直的判定定理和性质定理可说明
,由线面垂直的判定定理和性质定理可说明![]() ,由等腰三角形说明
,由等腰三角形说明![]() ,进而可证
,进而可证![]() 平面
平面![]() ,
,![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,最后在
的平面角,最后在![]() 中求得答案.
中求得答案.
(1)证明:(法一)
如图取![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() ,
,
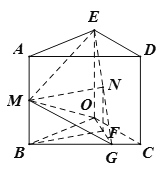
则在![]() 中由中位线定理可知
中由中位线定理可知![]() 且
且![]() ,
,
又由原正方形可得![]() 且
且![]()
![]() 且
且![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
法二:
如图,延长![]() 、
、![]() 交于点
交于点![]() ,连结
,连结![]() ,
,
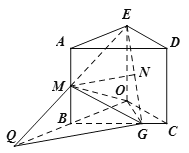
![]() 且
且![]() ,
,
![]() ,
,
![]() 为
为![]() 中点,
中点,
中位线![]()
又![]() 平面
平面![]() ,
,![]() 面
面![]() ,
,
![]() 平面
平面![]() .
.
(2)解:(法一)
如图,因为![]() ,
,![]() ,
,

所以![]() ,
,
又![]() .所以
.所以![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() 面
面![]() ,
,![]()
又![]() 为
为![]() 中点,即
中点,即![]() ,所以
,所以![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.
法二:
如图,![]() ,
,![]() ,
,
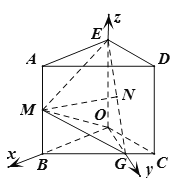
![]() ,
,
又![]() .所以
.所以![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() .
.
又![]() ,
,
![]() 平面
平面![]() ,
,![]() 面
面![]() ,
,![]()
建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
而![]() 是平面
是平面![]() 的一个法向量
的一个法向量
设平面![]() 的法向量为
的法向量为![]() ,
,
由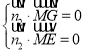 ,即
,即 ,
,
令![]() ,则
,则![]() ,
,![]()
面![]() 的一个法向量为
的一个法向量为![]() ,
,
设二面角![]() 大小为
大小为![]() ,由图,
,由图,![]() .
.
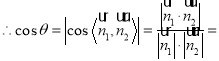
![]() .
.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重![]() ,次品重
,次品重![]() ,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第
,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() ),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() _________
_________![]() ;若次品所在的袋子的编号是
;若次品所在的袋子的编号是![]() ,此时的重量
,此时的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
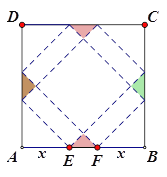
【题目】请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得![]() 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm2
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm2
(1)若广告商要求包装盒侧面积S(cm![]() )最大,试问x应取何值?
)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm![]() )最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把编号为1,2,3,4,5的五个大小、形状相同的小球,随机放入编号为1,2,3,4,5的五个盒子里.每个盒子里放入一个小球.
(1)求恰有两个球的编号与盒子的编号相同的概率;
(2)设恰有![]() 个小球的编号与盒子编号相同,求随机变量
个小球的编号与盒子编号相同,求随机变量![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线C:y2=8x上一点A到焦点F的距离为6,若点P为抛物线C准线上的动点,则|OP|+|AP|的最小值为( )
A. 4B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数
垂直,求函数![]() 在
在![]() 点处的切线方程;
点处的切线方程;
(2)若对于![]() ,
,![]() 恒成立,求正实数
恒成立,求正实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,且函数
,且函数![]() 有极大值点
有极大值点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】谢宾斯基三角形是一种分形,由波兰数学家谢宾斯基在1915年提出,先作一个正三角形.挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的小三角形中又挖去一个“中心三角形”,我们用白色代表挖去的面积,那么黑三角形为剩下的面积(我们称黑三角形为谢宾斯基三角形).向图中第5个大正三角形中随机撒512粒大小均匀的细小颗粒物,则落在白色区域的细小颗粒物的数量约是( )

A.256B.350C.162D.96
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com