练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．已知每生产100克饼干的原材料加工费为1.8元，某食品加工厂对饼干采用两种包装，其包装费用、销售价格如表所示：
    型号小包装大包装
    重量100克300克
    包装费0.5元0.7元
    销售价格3.00元8.4元
    则下列说法正确的是（　　）
    ①买小包装实惠；②买大包装实惠；③卖3小包比卖1大包盈利多；④卖1大包比卖3小包盈利多．
    A．①②B．①④C．②③D．②④

    分析 分别求出大包装和小包装每100克的价格进行比较，以及卖1大包和3小包的盈利即可得到结论．

    解答 解：大包装300克8.4元，
    则等价为100克2.8元，小包装100克3元，
    则买大包装实惠，故②正确，
    卖1大包装盈利8.4-0.7-1.8×3=2.3元，
    卖1小包装盈利3-0.5-1.8=0.7，
    则卖3小包盈利0.7×3=2.1元，
    则卖1大包比卖3小包盈利多．故④正确，
    故选：D

    点评 本题主要考查函数模型的应用，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．椭圆C的左、右焦点为F1（-1，0）、F2（1，0），且点P（1，$\frac{2\sqrt{3}}{3}$）在椭圆C上．
    （1）求椭圆C的方程；
    （2）设过F1的动直线l交椭圆C于A，B两点，求△F2AB面积的最大值及面积最大时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．在空间四边形ABCD中，AB⊥AC，AB⊥BD，AC=2，AB=BD=1，AC与BD所成的角为60°，则CD=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$），f（x）的部分图象如图示，则关于y=f（x）错误的是（　　）
    A．最小正周期为π
    B．向右平移$\frac{π}{6}$个单位得到函数y=sin（2x-$\frac{π}{6}$）
    C．在区间[0，$\frac{π}{2}$]上的值域为[-$\frac{1}{2}，\frac{1}{2}$]
    D．向左平移$\frac{π}{6}$个单位得到的图象关于y轴对称

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．双曲线${x^2}-\frac{y^2}{m}=1$的离心率大于$\sqrt{2}$，则（　　）
    A．$m＞\frac{1}{2}$B．m≥1C．m＞1D．m＞2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知数列{an}中，a1=3，a2=5，且对于任意的大于2的正整数n，有an=an-1-an-2，则a2015=-5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．数列{an}满足a1=1，且对于任意的n∈N*都满足an+1=$\frac{{a}_{n}}{3{a}_{n}+1}$，则数列{anan+1}的前n项和为 （　　）
    A．$\frac{1}{3n+1}$B．$\frac{n}{3n+1}$C．$\frac{1}{3n-2}$D．$\frac{n}{3n-2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．过椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点F1（-$\sqrt{3}$，0），而且过点C（$\sqrt{3}$，$\frac{1}{2}$）
    （1）求椭圆E的方程：
    （2）过点C的直线l与椭圆E的另一交点为D，与y轴的交点为B．过原点O且平行于l的直线与椭圆的一个交点为H．若CD•CB=2OH2，求直线l的方程．
    （3）设椭圆E的上下顶点分别为A1，A2，P是椭圆上异于A1，A2的任一点，直线PA1，PA2分别交x轴于点N，M，若直线0T与过点M，N的圆G相切，切点为T．线段0T的长是否为定值，若是并求出该定值，不是说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

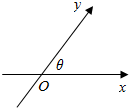    3．如图，数轴x，y的交点为O，夹角为θ，与x轴、y轴正向同向的单位向量分别是$\overrightarrow{e_1}，\overrightarrow{e_2}$．由平面向量基本定理，对于平面内的任一向量$\overrightarrow{OP}$，存在唯一的有序实数对（x，y），使得$\overrightarrow{OP}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$，我们把（x，y）叫做点P在斜坐标系xOy中的坐标（以下各点的坐标都指在斜坐标系xOy中的坐标）．
    （1）若θ=90°，$\overrightarrow{OP}$为单位向量，且$\overrightarrow{OP}$与$\overrightarrow{e_1}$的夹角为120°，求点P的坐标；
    （2）若θ=45°，点P的坐标为$（{1，\sqrt{2}}）$，求向量$\overrightarrow{OP}$与$\overrightarrow{e_1}$的夹角；
    （3）若θ=60°，求过点A（2，1）的直线l的方程，使得原点O到直线l的距离最大．

    查看答案和解析>>

    同步练习册答案