
分析 对任意的x∈(0,$\frac{1}{2}$),4x≤logax恒成立,化为x∈(0,$\frac{1}{2}$)时,y=logax的图象恒在y=4x的图象的上方,
在同一坐标系中,分别画出两个函数的图象,由此求出实数a的取值范围.
解答 解:∵a∈(0,1)∪(1,+∞),
当x∈(0,$\frac{1}{2}$)时,函数y=4x的图象如下图所示: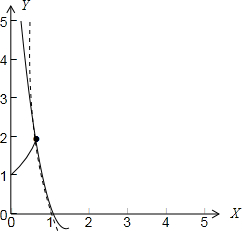
∵对任意的x∈(0,$\frac{1}{2}$)时,总有4x<logax恒成立,
若不等式4x<logax恒成立,则y=logax的图象恒在y=4x图象的上方(如图中虚线所示)
∵y=logax的图象与y=4x的图象交于($\frac{1}{2}$,2)点时,
a=$\frac{\sqrt{2}}{2}$,
故虚线所示的y=logax的图象对应的底数a应满足$\frac{\sqrt{2}}{2}$≤a<1.
故答案为:[$\frac{\sqrt{2}}{2}$,1).
点评 本题考查了指数函数、对数函数的图象与性质的应用问题,熟练掌握指数函数、对数函数的图象与性质是解题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 逆命题与逆否命题真,否命题假 | B. | 逆命题假,否命题和逆否命题真 | ||
| C. | 逆命题和否命题真,逆否命题假 | D. | 逆命题、否命题、逆否命题都真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| ξ | 10 | 20 | 30 |
| P | 0.6 | a | $\frac{1}{4}$-$\frac{a}{2}$ |
| A. | 42 | B. | 135 | C. | 402 | D. | 405 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
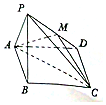 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
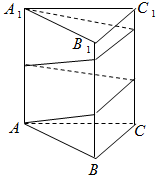 已知正三棱柱ABC-A1B1C1的底面边长为4cm,高为10cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为( )
已知正三棱柱ABC-A1B1C1的底面边长为4cm,高为10cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为( )| A. | 16cm | B. | 12$\sqrt{3}$cm | C. | 24$\sqrt{3}$cm | D. | 26cm |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1-3i}{2}$ | B. | $\frac{1+3i}{2}$ | C. | $\frac{-1-3i}{2}$ | D. | $\frac{-1+3i}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com