
 如图,四边形EFGH为四面体A-BCD的一个截面,若截面为平行四边形,
如图,四边形EFGH为四面体A-BCD的一个截面,若截面为平行四边形,分析 (1)由平行四边形性质得EF∥HG,从而EF∥平面ABD,进而EF∥AB,由此能证明AB∥平面EFGH.
(2)推导出CD∥EH,从而∠FEH即是AB和CD所成角,由此能证明平行四边形EFGH为矩形.
解答 证明:(1)∵EFGH为平行四边形,∴EF∥HG,(1分)
∵HG?平面ABD,EF?平面ABD
∴EF∥平面ABD.(3分)
∵EF?平面ABC,平面ABD∩平面ABC=AB.
∴EF∥AB,(5分)
EF?平面EFGH,AB?平面EFGH∴AB∥平面EFGH.(6分)
(2)同理可证:CD∥EH,(7分)
∴∠FEH即是AB和CD所成角 (8分)
∵AB⊥CD,∴∠FEH=90°(9分)
∴平行四边形EFGH为矩形.(10分)
点评 本题考查线面平行的证明,考查平行四边形为矩形的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
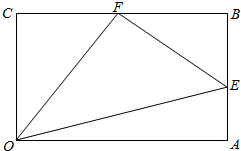 如图,某地要在矩形区域OABC内建造三角形池塘OEF,E,F分别在AB,BC边上,OA=5米,OC=4米,∠EOF=$\frac{π}{4}$,设CF=x,AE=y.
如图,某地要在矩形区域OABC内建造三角形池塘OEF,E,F分别在AB,BC边上,OA=5米,OC=4米,∠EOF=$\frac{π}{4}$,设CF=x,AE=y.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$)∪(3,+∞)) | B. | ($\frac{1}{2}$,3) | C. | (-3,-$\frac{1}{2}$) | D. | (-∞,-3)$∪(-\frac{1}{2},+∞)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com