
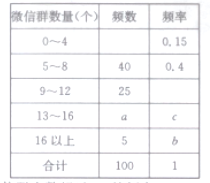
°æƒø°øæðÕ≥º∆£¨Ωÿ÷¡2016ƒÍµ◊»´π˙Œ¢–≈◊¢≤·”√ªß ˝¡ø“—æ≠Õª∆∆9.27“⁄.Œ™µ˜≤È¥Û—ß…˙’‚∏ˆŒ¢–≈”√ªß»∫ÃÂ÷–√ø»À”µ”–Œ¢–≈»∫µƒ ˝¡ø£¨œ÷¥”ƒ≥ –¥Û—ß…˙÷–Àʪ˙≥È»°100ŒªÕ¨—ßΩ¯––¡À≥È—˘µ˜≤È£¨Ω·π˚»Áœ¬£∫
£®1£©«Û![]() £¨
£¨![]() £¨
£¨![]() µƒ÷µº∞—˘±æ÷–Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∏≈¬ £ª
µƒ÷µº∞—˘±æ÷–Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∏≈¬ £ª
£®2£©»Ù¥”’‚100ŒªÕ¨—ß÷–Àʪ˙≥È»°2»À£¨«Û’‚2»À÷–«°”–1»ÀŒ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∏≈¬ £ª
£®3£©“‘£®1£©÷–µƒ∆µ¬ ◊˜Œ™∏≈¬ £¨»Ù¥”»´ –¥Û—ß…˙÷–Àʪ˙≥È»°3»À£¨º«![]() ±Ì æ≥ÈµΩµƒ «Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ»À ˝£¨«Û
±Ì æ≥ÈµΩµƒ «Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ»À ˝£¨«Û![]() µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚
µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚![]() .
.
°æ¥∞∏°ø£®1£©![]() .£®2£©
.£®2£©![]() .£®3£©º˚Ω‚Œˆ
.£®3£©º˚Ω‚Œˆ
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫
(1)¿˚”√∆µ¬ ∑÷≤º±Ìø…µ√![]() £¨
£¨![]() £¨
£¨![]() .‘ÚŒ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∆µ¬ Œ™
.‘ÚŒ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∆µ¬ Œ™![]() .
.
(2)”…“‚ø…µ√2»À÷–«°”–1»ÀŒ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∏≈¬ Œ™![]() .
.
(3)”…“‚ø…µ√![]() µƒÀ˘”–ø…ƒÐ»°÷µ0£¨1£¨2£¨3.Ω·∫œ∏≈¬ π´ Ω∫Õ∂˛œÓ∑÷≤ºµƒπ´ Ωº¥ø…«Ûµ√∑÷≤º¡–£¨»ª∫Û«ÛΩ‚ ˝—ß∆⁄Õ˚ø…µ√
µƒÀ˘”–ø…ƒÐ»°÷µ0£¨1£¨2£¨3.Ω·∫œ∏≈¬ π´ Ω∫Õ∂˛œÓ∑÷≤ºµƒπ´ Ωº¥ø…«Ûµ√∑÷≤º¡–£¨»ª∫Û«ÛΩ‚ ˝—ß∆⁄Õ˚ø…µ√![]() .
.
‘Ã‚Ω‚Œˆ£∫
£®1£©‘⁄0÷¡4∏ˆ’‚“ª∂Œ£¨∂‘”¶µƒ∆µ ˝Œ™15£¨
”…“—÷™µ√£∫![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
°ý![]() £¨
£¨![]() .Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∆µ¬ Œ™
.Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∆µ¬ Œ™![]() .
.
£®2£©º«°∞2»À÷–«°”–1»ÀŒ¢–≈»∫∏ˆ ˝≥¨π˝12°±Œ™ ¬º˛![]() £¨‘Ú
£¨‘Ú![]() .
.
À˘“‘£¨2»À÷–«°”–1»ÀŒ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∏≈¬ Œ™![]() .
.
£®3£©“¿Ã‚“‚ø…÷™£¨Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∏≈¬ Œ™![]() .
.
![]() µƒÀ˘”–ø…ƒÐ»°÷µ0£¨1£¨2£¨3.
µƒÀ˘”–ø…ƒÐ»°÷µ0£¨1£¨2£¨3.
‘Ú![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨![]() .
.
∆‰∑÷≤º¡–»Áœ¬£∫
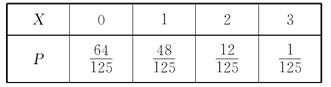
À˘“‘£¨![]()
![]() £¨ªÚ
£¨ªÚ![]() .
.


 ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏
ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏ –°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
–°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ ˝¡–![]() µƒÕ®œÓπ´ Ω «
µƒÕ®œÓπ´ Ω «![]() £Æ
£Æ
£®1£©≈–∂œ![]() «∑Ò « ˝¡–
«∑Ò « ˝¡–![]() ÷–µƒœÓ£ª
÷–µƒœÓ£ª
£®2£© ‘≈–∂œ ˝¡–![]() ÷–µƒ∏˜œÓ «∑Ò∂º‘⁄«¯º‰
÷–µƒ∏˜œÓ «∑Ò∂º‘⁄«¯º‰![]() ƒ⁄£ª
ƒ⁄£ª
£®3£© ‘≈–∂œ‘⁄«¯º‰![]() ƒ⁄ «∑Ò”–ŒÞ«Ó ˝¡–
ƒ⁄ «∑Ò”–ŒÞ«Ó ˝¡–![]() ÷–µƒœÓ£ø»Ù”–£¨ «µ⁄º∏œÓ£ø»Ù√ª”–£¨«ÎÀµ√˜¿Ì”…£Æ
÷–µƒœÓ£ø»Ù”–£¨ «µ⁄º∏œÓ£ø»Ù√ª”–£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº«»´ºØU={1£¨2£¨3£¨4£¨5£¨6£¨7£¨8}£¨A={1£¨2£¨3£¨5}£¨B={2£¨4£¨6}£¨‘ÚÕº÷–“ı”∞≤ø∑÷À˘±Ì 浃ºØ∫œ «£® £© 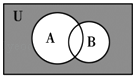
A.{4£¨6£¨7£¨8}
B.{2}
C.{7£¨8}
D.{1£¨2£¨3£¨4£¨5£¨6}
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
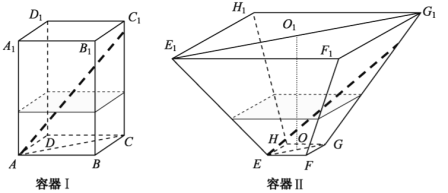
°æƒø°ø»ÁÕº£¨ÀÆ∆Ω∑≈÷√µƒ’˝Àƒ¿‚÷˘–Œ≤£¡ß»ð∆˜¢Ò∫Õ’˝Àƒ¿‚î–Œ≤£¡ß»ð∆˜¢Úµƒ∏þæ˘Œ™32cm£¨»ð∆˜¢Òµƒµ◊√Ê∂‘Ω«œþACµƒ≥§Œ™10![]() cm£¨»ð∆˜¢Úµƒ¡Ωµ◊√Ê∂‘Ω«œþ
cm£¨»ð∆˜¢Úµƒ¡Ωµ◊√Ê∂‘Ω«œþ![]() £¨
£¨![]() µƒ≥§∑÷±Œ™14cm∫Õ62cm£Æ∑÷±‘⁄»ð∆˜¢Ò∫Õ»ð∆˜¢Ú÷–◊¢»ÎÀÆ£¨ÀÆ…Óæ˘Œ™12cm£Æœ÷”–“ª∏˘≤£¡ß∞Ùl£¨∆‰≥§∂»Œ™40cm£Æ£®»ð∆˜∫Ò∂»°¢≤£¡ß∞Ù¥÷œ∏æ˘∫ˆ¬‘≤ªº∆£©
µƒ≥§∑÷±Œ™14cm∫Õ62cm£Æ∑÷±‘⁄»ð∆˜¢Ò∫Õ»ð∆˜¢Ú÷–◊¢»ÎÀÆ£¨ÀÆ…Óæ˘Œ™12cm£Æœ÷”–“ª∏˘≤£¡ß∞Ùl£¨∆‰≥§∂»Œ™40cm£Æ£®»ð∆˜∫Ò∂»°¢≤£¡ß∞Ù¥÷œ∏æ˘∫ˆ¬‘≤ªº∆£©
£®1£©Ω´![]() ∑≈‘⁄»ð∆˜¢Ò÷–£¨
∑≈‘⁄»ð∆˜¢Ò÷–£¨![]() µƒ“ª∂À÷√”⁄µ„A¥¶£¨¡Ì“ª∂À÷√”⁄≤ý¿‚
µƒ“ª∂À÷√”⁄µ„A¥¶£¨¡Ì“ª∂À÷√”⁄≤ý¿‚![]() …œ£¨«Û
…œ£¨«Û![]() √ª»ÎÀÆ÷–≤ø∑÷µƒ≥§∂»£ª
√ª»ÎÀÆ÷–≤ø∑÷µƒ≥§∂»£ª
£®2£©Ω´![]() ∑≈‘⁄»ð∆˜¢Ú÷–£¨
∑≈‘⁄»ð∆˜¢Ú÷–£¨![]() µƒ“ª∂À÷√”⁄µ„E¥¶£¨¡Ì“ª∂À÷√”⁄≤ý¿‚
µƒ“ª∂À÷√”⁄µ„E¥¶£¨¡Ì“ª∂À÷√”⁄≤ý¿‚![]() …œ£¨«Û
…œ£¨«Û![]() √ª»ÎÀÆ÷–≤ø∑÷µƒ≥§∂»£Æ
√ª»ÎÀÆ÷–≤ø∑÷µƒ≥§∂»£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∏¯∂®∫Ø ˝£∫¢Ÿ ![]() £¨¢⁄
£¨¢⁄ ![]() £¨¢€y=|x2©Å2x|£¨¢Ðy=x+
£¨¢€y=|x2©Å2x|£¨¢Ðy=x+ ![]() £¨∆‰÷–‘⁄«¯º‰£®0£¨1£©…œµ•µ˜µðºıµƒ∫Ø ˝–Ú∫≈ «£® £©
£¨∆‰÷–‘⁄«¯º‰£®0£¨1£©…œµ•µ˜µðºıµƒ∫Ø ˝–Ú∫≈ «£® £©
A.¢⁄¢Ð
B.¢⁄¢€
C.¢Ÿ¢€
D.¢Ÿ¢Ð
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø—°–Þ4-4£∫◊¯±Íœµ”Î≤Œ ˝∑Ω≥Ã
“‘◊¯±Í‘≠µ„![]() Œ™º´µ„£¨“‘
Œ™º´µ„£¨“‘![]() ÷·’˝∞Î÷·Œ™º´÷·£¨Ω®¡¢º´◊¯±Íœµ£¨¡Ω÷÷◊¯±Íœµ÷–»°œýÕ¨µƒ≥§∂»µ•Œª£¨÷±œþ
÷·’˝∞Î÷·Œ™º´÷·£¨Ω®¡¢º´◊¯±Íœµ£¨¡Ω÷÷◊¯±Íœµ÷–»°œýÕ¨µƒ≥§∂»µ•Œª£¨÷±œþ![]() µƒ≤Œ ˝∑Ω≥ÃŒ™
µƒ≤Œ ˝∑Ω≥ÃŒ™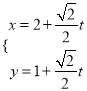 £®
£®![]() Œ™≤Œ ˝£©£¨‘≤
Œ™≤Œ ˝£©£¨‘≤![]() µƒº´◊¯±Í∑Ω≥ÃŒ™
µƒº´◊¯±Í∑Ω≥ÃŒ™![]() .
.
£®1£©«Û÷±œþ![]() µƒ∆’Õ®∑Ω≥ÔΑ≤
µƒ∆’Õ®∑Ω≥ÔΑ≤![]() µƒ÷±Ω«◊¯±Í∑Ω≥ãª
µƒ÷±Ω«◊¯±Í∑Ω≥ãª
£®2£©…Ë‘≤![]() ”Î÷±œþ
”Î÷±œþ![]() Ωª”⁄
Ωª”⁄![]() ¡Ωµ„£¨»Ùµ„
¡Ωµ„£¨»Ùµ„![]() µƒ÷±Ω«◊¯±ÍŒ™
µƒ÷±Ω«◊¯±ÍŒ™![]() £¨«Û
£¨«Û![]() µƒ÷µ.
µƒ÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂®“‘⁄R…œµƒ≈º∫Ø ˝f£®x£©£¨µ±x°ð0 ±£¨f£®x£©=x2©Å4x
£®1£©«Ûf£®©Å2£©µƒ÷µ£ª
£®2£©µ±x£º0 ±£¨«Ûf£®x£©µƒΩ‚Œˆ Ω£ª
£®3£©…Ë∫Ø ˝f£®x£©‘⁄[t©Å1£¨t+1]£®t£æ1£©…œµƒ◊Ó¥Û÷µŒ™g£®t£©£¨«Ûg£®t£©µƒ◊Ó–°÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() «“
«“![]() .
.
£®I£©»Ù![]() £¨«Û∫Ø ˝
£¨«Û∫Ø ˝![]() µƒµ•µ˜«¯º‰£ª£®∆‰÷–
µƒµ•µ˜«¯º‰£ª£®∆‰÷–![]() «◊‘»ª∂‘ ˝µƒµ◊ ˝£©
«◊‘»ª∂‘ ˝µƒµ◊ ˝£©
£®II£©…Ë∫Ø ˝![]() £¨µ±
£¨µ±![]() ±£¨«˙œþ
±£¨«˙œþ![]() ”Î
”Î![]() ”–¡Ω∏ˆΩªµ„£¨«Û
”–¡Ω∏ˆΩªµ„£¨«Û![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() £∫
£∫ ![]() µƒ¿Î–ƒ¬
µƒ¿Î–ƒ¬ ![]() £¨π˝Õ÷‘≤µƒ◊ÛΩπµ„
£¨π˝Õ÷‘≤µƒ◊ÛΩπµ„![]() «“«„–±Ω«Œ™
«“«„–±Ω«Œ™![]() µƒ÷±œþ”Α≤
µƒ÷±œþ”Α≤![]() œýΩªÀ˘µ√œ“µƒ≥§∂»Œ™1.
œýΩªÀ˘µ√œ“µƒ≥§∂»Œ™1.
£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©»Ù÷±œþ![]() ΩªÕ÷‘≤”⁄≤ªÕ¨µƒ¡Ωµ„
ΩªÕ÷‘≤”⁄≤ªÕ¨µƒ¡Ωµ„![]() £¨…Ë
£¨…Ë![]() £¨
£¨ ![]() £¨∆‰÷–
£¨∆‰÷–![]() Œ™◊¯±Í‘≠µ„.µ±“‘œþ∂Œ
Œ™◊¯±Í‘≠µ„.µ±“‘œþ∂Œ![]() Œ™÷±æ∂µƒ‘≤«°∫√π˝µ„
Œ™÷±æ∂µƒ‘≤«°∫√π˝µ„![]() ±£¨«Û÷§£∫
±£¨«Û÷§£∫ ![]() µƒ√ʪ˝Œ™∂®÷µ£¨≤¢«Û≥ˆ∏√∂®÷µ.
µƒ√ʪ˝Œ™∂®÷µ£¨≤¢«Û≥ˆ∏√∂®÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com