
下列命题:
①命题“事件A与B互斥”是“事件A与B对立”的必要不充分条件;
②“am2<bm2”是“a<b”的充分必要条件;
③“矩形的两条对角线相等”的否命题为假;
④在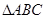 中,“
中,“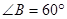 ”是
”是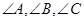 三个角成等差数列的充要条件;
三个角成等差数列的充要条件;
⑤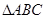 中,若
中,若 ,则
,则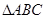 为直角三角形.
为直角三角形.
判断错误的有___________.
②⑤
【解析】
试题分析:事件A与B互斥,事件A与B不一定对立;反之事件A与B对立,一定有事件A与B互斥.所以“事件A与B互斥”是“事件A与B对立”的必要不充分条件.所以命题①正确.由am2<bm2知m2>0,不等式两边同乘以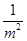 得,a<b,反之,若a<b,则取m2=0时不能得到am2<bm2,故am2<bm2是a<b的充分不必要条件,故命题②不正确.原命题:矩形的两条对角线相等.则其否命题为:若四边形不是矩形,则其对角线不相等.此否命题为假命题,如等腰梯形不是矩形,但其对角线相等,故命题③正确.在△ABC中,若∠B=60°,因为∠A+∠B+∠C=180°,得∠A+∠C=180°-∠B=180°-60°=120°,所以2∠B=∠A+∠C,所以∠A,∠B,∠C三个角成等差数列.若∠A,∠B,∠C三个角成等差数列,可设公差为d,则∠A=∠B-d,∠C=∠B+d,由∠A+∠B+∠C=180°,得∠B-d+∠B+∠b+d=180°,∴∠B=60°.所以在△ABC中,“∠B=60°”是∠A,∠B,∠C三个角成等差数列的充要条件,故命题④正确.在△ABC中,若sinA=cosB,则sinA=sin(90°-B),所以A=90°-B或A+90°-B=180°,所以A+B=90°或A-B=90°,则△ABC不一定为直角三角形,故命题⑤不正确.故答案为②⑤.
得,a<b,反之,若a<b,则取m2=0时不能得到am2<bm2,故am2<bm2是a<b的充分不必要条件,故命题②不正确.原命题:矩形的两条对角线相等.则其否命题为:若四边形不是矩形,则其对角线不相等.此否命题为假命题,如等腰梯形不是矩形,但其对角线相等,故命题③正确.在△ABC中,若∠B=60°,因为∠A+∠B+∠C=180°,得∠A+∠C=180°-∠B=180°-60°=120°,所以2∠B=∠A+∠C,所以∠A,∠B,∠C三个角成等差数列.若∠A,∠B,∠C三个角成等差数列,可设公差为d,则∠A=∠B-d,∠C=∠B+d,由∠A+∠B+∠C=180°,得∠B-d+∠B+∠b+d=180°,∴∠B=60°.所以在△ABC中,“∠B=60°”是∠A,∠B,∠C三个角成等差数列的充要条件,故命题④正确.在△ABC中,若sinA=cosB,则sinA=sin(90°-B),所以A=90°-B或A+90°-B=180°,所以A+B=90°或A-B=90°,则△ABC不一定为直角三角形,故命题⑤不正确.故答案为②⑤.
考点:本题考查了判断命题的真假及充要条件判断.
点评:最常用的方法是定义法,即“若p?q,则p是q的充分条件”;“若q?p,则p是q成立的必要条件”;“若p?q,则p是q的充要条件”


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| OP |
| OA |
| OB |
| OC |
| AB |
| AC |
| AB |
| AC |
查看答案和解析>>
科目:高中数学 来源:宁夏银川一中2012届高三第一次模拟考试数学文科试题 题型:013
有下列命题:
①设集合M={x|0<x≤3},N={x|0<x≤2},则“a∈M”是“a∈N”的充分而不必要条件;
②命题“若a∈M,则b![]() M”的逆否命题是:若b∈M,则a
M”的逆否命题是:若b∈M,则a![]() M;
M;
③若p∧q是假命题,则p,q都是假命题;
④命题P:“![]() x0∈R,
x0∈R,![]() -x0-1>0”的否定
-x0-1>0”的否定![]() :“
:“![]() x∈R,x2-x-1≤0”
x∈R,x2-x-1≤0”
则上述命题中为真命题的是
A.①②③④
B.①③④
C.②④
D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com