
| A. | (2,2) | B. | ($\sqrt{6}$,3) | C. | (3,$\sqrt{6}$) | D. | ($\frac{9}{2}$,3) |
分析 作PM⊥准线l,M为垂足,由抛物线的定义可得|PF|-|PA|=|PM|-|PA|,故当P,A,M三点共线时,|PF|-|PA|最大为|AM|,此时,P点的纵坐标为3,代入抛物线的方程可求得P点的横坐标,从而得到P点的坐标.
解答 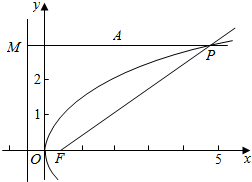 解:由题意可得F($\frac{1}{2}$,0 ),
解:由题意可得F($\frac{1}{2}$,0 ),
准线方程为x=-$\frac{1}{2}$,
作PM⊥准线l,M为垂足,
由抛物线的定义可得|PF|-|PA|=|PM|-|PA|,
故当P,A,M三点共线时,|PF|-|PA|取得最大值,
且为|AM|=2-(-$\frac{1}{2}$)=$\frac{5}{2}$,
此时,P点的纵坐标为3,
代入抛物线的方程可求得P点的横坐标为$\frac{9}{2}$,
故P点的坐标为($\frac{9}{2}$,3),
故选:D.
点评 本题主要考查抛物线的定义、标准方程,以及简单性质的应用,判断当P,A,M三点共线时,|PF|-|PA|最大为|AM|,是解题的关键,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
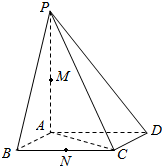 四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,AB=PA=2,M,N分别为PA,PB的中点,则MD与AN所成角的余弦值为$\frac{2}{5}$.
四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,AB=PA=2,M,N分别为PA,PB的中点,则MD与AN所成角的余弦值为$\frac{2}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 5 | D. | $\frac{15}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
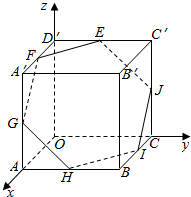 正方体OABC-D′A′B′C′的棱长为a,E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,写出正六边形EFGHIJ各顶点的坐际.
正方体OABC-D′A′B′C′的棱长为a,E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,写出正六边形EFGHIJ各顶点的坐际.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com