Question

8．已知实数x，y满足：x³+2xy-1=0（-1≤x≤2，x≠0），这个方程确定的函数为y=f（x），若函数z=3x+2f（x）-k有且只有一个零点，则实数k的取值范围是$（-∞，-5）∪\right\{-\frac{15}{4}\left\}∪（\frac{5}{2}，+∞）$．

Answer 1

分析 由已知可得函数z=3x+2f（x）-k=$\frac{-{x}^{3}+3{x}^{2}+1}{x}$-k，（-1≤x≤2，x≠0），若函数z=3x+2f（x）-k有且只有一个零点，则函数y=$\frac{-{x}^{3}+3{x}^{2}+1}{x}$，（-1≤x≤2，x≠0）的图象，与y=k有且只有一个交点，数形结合，可得答案．

解答 解：∵方程x³+2xy-1=0，（-1≤x≤2，x≠0）确定的函数为y=f（x），
∴f（x）=$\frac{-{x}^{3}+1}{2x}$，（-1≤x≤2，x≠0），
∴函数z=3x+2f（x）-k=$\frac{-{x}^{3}+3{x}^{2}+1}{x}$-k，（-1≤x≤2，x≠0），
若函数z=3x+2f（x）-k有且只有一个零点，
则函数y=$\frac{-{x}^{3}+3{x}^{2}+1}{x}$，（-1≤x≤2，x≠0）的图象，与y=k有且只有一个交点，
∵y′=$\frac{-2{x}^{3}+3{x}^{2}-1}{{x}^{2}}$，
令y′=0，则x=1，或x=-$\frac{1}{2}$，
当-1≤x＜-$\frac{1}{2}$时，y′＞0，函数为增函数，-$\frac{1}{2}$＜x＜0，或0＜x≤2时，y′≤0，函数为减函数，
故函数y=$\frac{-{x}^{3}+3{x}^{2}+1}{x}$的草图如下所示：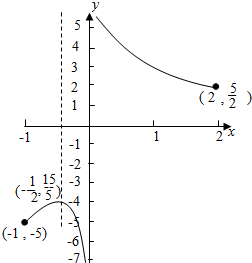

由图可得：k∈$（-∞，-5）∪\right\{-\frac{15}{4}\left\}∪（\frac{5}{2}，+∞）$，
故答案为：$（-∞，-5）∪\right\{-\frac{15}{4}\left\}∪（\frac{5}{2}，+∞）$．

点评 本题考查的知识点是数形结合问题，将函数的零点个数，转化为函数图象与直线的交点个数是解答的关键．