
 与向量
与向量 共线,且满足
共线,且满足 ,
, ,则
,则 = ,k= .
= ,k= .  ,我们可以根据向量
,我们可以根据向量 与向量
与向量 共线,且满足
共线,且满足 ,结合向量共线的性质,构造方程进行解答,再由
,结合向量共线的性质,构造方程进行解答,再由 结合向量垂直的性质,构造关于K的方程,解方程即可求出K值.
结合向量垂直的性质,构造关于K的方程,解方程即可求出K值. 与向量
与向量 共线,
共线, ,
, 与向量
与向量 同向
同向 ,则
,则 =
=
 =(4,-2,4)
=(4,-2,4)

 =0
=0 ,此时向量的数量积,等于0.判断两个向量的关系(平行或垂直)或是已知两个向量的关系求未知参数的值,要熟练掌握向量平行(共线)及垂直的坐标运算法则,即“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0”.
,此时向量的数量积,等于0.判断两个向量的关系(平行或垂直)或是已知两个向量的关系求未知参数的值,要熟练掌握向量平行(共线)及垂直的坐标运算法则,即“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0”. 

科目:高中数学 来源:2012-2013学年重庆市高三上学期半期考试理科数学试卷(解析版) 题型:解答题
已知函数
(1)当 时,求函数
时,求函数 的最小值和最大值;
的最小值和最大值;
(2)设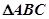 的内角
的内角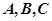 的对应边分别为
的对应边分别为 ,且
,且 ,若向量
,若向量 与向量
与向量 共线,求
共线,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三上学期第四次月考数学文卷 题型:解答题
(12分)在平面直角坐标系中,O为坐标原点,已知向量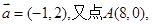
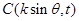
 与向量
与向量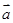 共线。
共线。
(1)求t所满足的关系式;
(2)当k>4且 取最大值为4时,求
取最大值为4时,求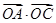 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:0123 期末题 题型:解答题
在平面直角坐标系中,O为坐标原点,已知向量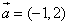 ,点A(8,0),B(n,t),
,点A(8,0),B(n,t),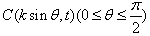 。
。
(1)若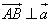 ,且
,且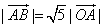 ,求向量
,求向量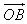 ;
;
(2)若向量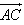 与向量
与向量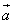 共线,当k>4时,tsinθ的最大值为4,求
共线,当k>4时,tsinθ的最大值为4,求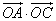 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2011届江西省上高二中高三上学期第四次月考数学文卷 题型:解答题
(12分)在平面直角坐标系中,O为坐标原点,已知向量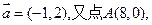
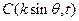
 与向量
与向量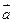 共线。
共线。
(1)求t所满足的关系式;
(2)当k>4且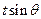 取最大值为4时,求
取最大值为4时,求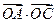 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com