
【题目】设椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,上顶点为A,在x轴负半轴上有一点B,满足
,上顶点为A,在x轴负半轴上有一点B,满足![]() 为线段
为线段![]() 的中点,且AB⊥
的中点,且AB⊥![]() 。
。
(I)求椭圆C的离心率;
(II)若过A、B、![]() 三点的圆与直线
三点的圆与直线![]() :
:![]() 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(III)在(I)的条件下,过右焦点![]() 作斜率为k的直线与椭圆C交于M,N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,说明理由。
作斜率为k的直线与椭圆C交于M,N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,说明理由。
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 。
。
【解析】分析:(Ⅰ)由题意可得在在直角三角形![]() 中有
中有![]() ,即
,即![]() ,整理可得
,整理可得![]() .(Ⅱ)由题意可得过A、B、F2三点的圆的圆心为F1(-c,0),半径r=
.(Ⅱ)由题意可得过A、B、F2三点的圆的圆心为F1(-c,0),半径r=![]()
=2c,根据直线![]() 与圆相切可得
与圆相切可得![]() ,解得c=1,从而
,解得c=1,从而![]() ,
,![]() ,可得椭圆的方程.(Ⅲ)由条件可设直线MN的方程为
,可得椭圆的方程.(Ⅲ)由条件可设直线MN的方程为![]() ,与椭圆方程联立消元后得到一元二次方程,结合根据系数的关系可得MN的中点Q的坐标为
,与椭圆方程联立消元后得到一元二次方程,结合根据系数的关系可得MN的中点Q的坐标为![]() ,若以PM,PN为邻边的平行四边形是菱形,则
,若以PM,PN为邻边的平行四边形是菱形,则![]() ,由此得到
,由此得到![]() ,整理得
,整理得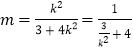 ,最后可求得
,最后可求得![]() .
.
详解:(I)∵AB⊥AF2,![]() 为
为![]() 的中点,
的中点,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即椭圆C的离心率为![]() .
.
(II)过A、B、F2三点的圆的圆心为F1(-c,0),半径r=![]() =2c.
=2c.
∵直线![]() :
:![]() 相切,
相切,
∴![]() ,
,
解得c=1.
又![]() ,
,
∴![]() ,
,
∴![]() .
.
∴椭圆C的方程为![]() .
.
(III)由(I)知,F2(1,0),直线MN的方程为![]() ,
,
由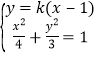 消去y整理得
消去y整理得![]()
∵直线与椭圆C交于M,N两点,
∴![]() .
.
设M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),
),
则![]()
∴![]() ,
,
∴MN的中点Q的坐标为![]() ,
,
若以PM,PN为邻边的平行四边形是菱形,
则![]() ,
,
∴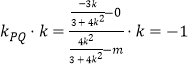
整理得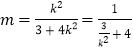 ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
故存在满足题意的点P,且m的取值范围是(![]() .
.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为![]() .
.
(1)求椭圆![]() 的方程式;
的方程式;
(2)已知动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
①若线段![]() 中点的横坐标为
中点的横坐标为![]() ,求斜率
,求斜率![]() 的值;
的值;
②已知点![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,且两种坐标系中采取相同的单位长度.曲线
轴的正半轴为极轴,建立极坐标系,且两种坐标系中采取相同的单位长度.曲线![]() 的极坐标方程是
的极坐标方程是![]() ,直线的参数方程是
,直线的参数方程是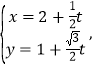 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的普通方程;
的普通方程;
(2)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大型综艺节目,《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的![]() 根据调查显示,是否喜欢盲拧魔方与性别有关
根据调查显示,是否喜欢盲拧魔方与性别有关![]() 为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,得到的情况如表
为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,得到的情况如表![]() 所示,并邀请其中20名男生参加盲拧三阶魔方比赛,其完成情况如表
所示,并邀请其中20名男生参加盲拧三阶魔方比赛,其完成情况如表![]() 所示.
所示.


(Ⅰ)将表![]() 补充完整,并判断能否在犯错误的概率不超过
补充完整,并判断能否在犯错误的概率不超过![]() 的前提下认为是否喜欢盲拧与性别有关?
的前提下认为是否喜欢盲拧与性别有关?
(Ⅱ)现从表![]() 中成功完成时间在
中成功完成时间在![]() 和
和![]() 这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
附参考公式及数据: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲:82,81,79,78,95,88,93,84
乙:92,95,80,75,83,80,90,85
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)用分段函数的形式表示函数f(x);
(2)在平面直角坐标系中画出函数f(x)的图象;

(3)在同一平面直角坐标系中,再画出函数g(x)=![]() (x>0)的图象(不用列表),观察图象直接写出当x>0时,不等式f(x)>
(x>0)的图象(不用列表),观察图象直接写出当x>0时,不等式f(x)> ![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com