
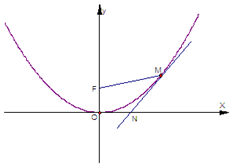
 如图,抛物线x2=4y在点$M(t,\;\frac{1}{4}{t^2})\;(t>0)$处的切线与x轴相交于点N,O、F分别为该抛物线的顶点、焦点.
如图,抛物线x2=4y在点$M(t,\;\frac{1}{4}{t^2})\;(t>0)$处的切线与x轴相交于点N,O、F分别为该抛物线的顶点、焦点.分析 (1)当t=2时,求导数,确定切线斜率,即可求切线MN的方程;
(2)过M作MH⊥x轴于H点,则H(t,0)又F(0,1),则S四边形OFMN=S梯形OFMH-S△MHN,即可求四边形OFMN的面积的最大值.
解答 解:(1)∵$y=\frac{1}{4}{x^2}∴y'=\frac{1}{2}x$…(2分),
∴y'|x=2=1即kMN=1…(3分)
又M(2,1)…(4分),
∴切线MN的方程是:y-1=1(x-2)…(5分)
即x-y-1=0…(6分)
(2)$y'\left|{_{x=t}=\frac{1}{2}t}\right.$,∴$MN的方程是:y-\frac{1}{4}{t^2}=\frac{1}{2}t(x-t)$ …(8分)
令$y=0得:x=\frac{1}{2}t∴N(\frac{1}{2}t,0)$…(9分)
过M作MH⊥x轴于H点,则H(t,0)又F(0,1)…(10分)
则S四边形OFMN=S梯形OFMH-S△MHN=$\frac{{1+\frac{1}{4}{t^2}}}{2}•t-\frac{1}{2}(t-\frac{t}{2})•\frac{1}{4}{t^2}$=$\frac{1}{16}{t^3}+\frac{1}{2}tt∈({0,1}]$ …(12分)
∵$S'=\frac{3}{16}{t^2}+\frac{1}{2}>0$,∴S(t)在(0,1]上为增函数 …(13分)
∴${S_{最大}}=S(1)=\frac{1}{16}+\frac{1}{2}=\frac{9}{16}$…(14分)
点评 本题考查直线、抛物线等基础知识,考查直线与抛物线的位置关系,考查运算求解能力,抽象思维能力,考查数形结合思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
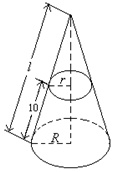 把一个圆锥截成圆台,已知圆台的上、下底面半径分别为1cm、4cm,母线长10cm.
把一个圆锥截成圆台,已知圆台的上、下底面半径分别为1cm、4cm,母线长10cm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
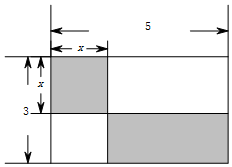 如图,一个长为5、宽为3的矩形被平行于边的两条直线所分割,其中矩形的左上角是一个是一个边长为x的正方形
如图,一个长为5、宽为3的矩形被平行于边的两条直线所分割,其中矩形的左上角是一个是一个边长为x的正方形查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com