已知数列an}的前n项和为sn,满足(p-1)sn=p2-an,其中p为正常数,且p≠1.
(1)求证:数列{an}为等比数列,并求出{an}的通项公式;
(2)若存在正整数M,使得当n≥M时,a1a4a7…a3n-2>a36恒成立,求出M的最小值;
(3)当p=2时,数列an,2xan+1,2yan+2成等差数列,其中x,y均为整数,求出x,y的值.
解:(1)因为(p-1)s
n=p
2-a
n,所以当n≥2时,(p-1)s
n-1=p
2-a
n-1,
两式相减得(p-1)a
n=a
n-a
n-1,即pa
n=a
n-1,所以
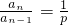
,
所以数列{a
n}为等比数列,公比为

,
又当n=1时,(p-1)s
1=p
2-a
1,即(p-1)a
1=p
2-a
1,所以
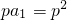
因为p>0,所以a
1=p,所以{a
n}的通项公式为:
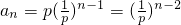
(2)由(1)知:a
1a
4a
7…a
3n-2=
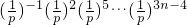
=
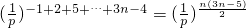
而
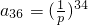
,所以不等式a
1a
4a
7…a
3n-2>a
36,即为
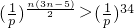
p为正常数,且p≠1,所以当0<p<1时,
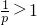
,所以
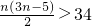
,解得n<-4或n>

,
故存在最小值为6的M,使得a
1a
4a
7…a
3n-2>a
36恒成立;
当p>1时,0<

<1,所以
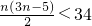
,解得-4<n<

,不合题意,
综合可得:当当0<p<1时,所求M的最小值为6.
(3)当p=2时,
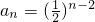
,因为数列a
n,2
xa
n+1,2
ya
n+2成等差数列,
所以
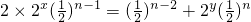
,
化简得2
x=1+2
y-2,显然x>y-2,因为x,y均为整数,
所以当y=2时,2
x=2,则x=1,
当y>2时,2
y-2为偶数,则1+2
y-2为奇数,即2
x为奇数,这与2
x为偶数矛盾,
当y<2时,2-y>0,x+2-y>0,由2
x=1+2
y-2得,2
x+2-y=1+2
2-y,则2
2-y为偶数,
1+2
2-y为奇数,即2
x+2-y为奇数,这与2
x+2-y为偶数矛盾,
综合得:x=1,y=2.
分析:(1)当n≥2时,(p-1)s
n-1=p
2-a
n-1,可得数列{a
n}为等比数列,公比为

,可求所以a
1=p,可得答案;
(2)由(1)可得
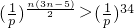
,分0<p<1和p>1两种情况来讨论;
(3)当p=2时,因为数列a
n,2
xa
n+1,2
ya
n+2成等差数列,可得2
x=1+2
y-2,通过对y进行讨论可得,当y=2时,2
x=2,则x=1;当y>2和y<2时,均会产生矛盾,故而得解.
点评:本题为等差、等比数列与不等式的综合应用,涉及分类讨论的思想,属中档题.

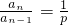 ,
, ,
,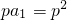
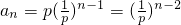
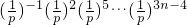 =
=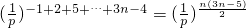
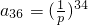 ,所以不等式a1a4a7…a3n-2>a36,即为
,所以不等式a1a4a7…a3n-2>a36,即为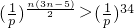
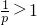 ,所以
,所以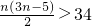 ,解得n<-4或n>
,解得n<-4或n> ,
, <1,所以
<1,所以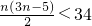 ,解得-4<n<
,解得-4<n< ,不合题意,
,不合题意,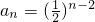 ,因为数列an,2xan+1,2yan+2成等差数列,
,因为数列an,2xan+1,2yan+2成等差数列,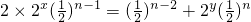 ,
, ,可求所以a1=p,可得答案;
,可求所以a1=p,可得答案;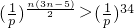 ,分0<p<1和p>1两种情况来讨论;
,分0<p<1和p>1两种情况来讨论;

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案