���𰸡�
��������1����i�����������f��x���ĵ�����f�䣨x����Ȼ������ճ�f�䣨x��=h��x����x
2-bx+1��������ʽ����˵��h��x���������x�ʣ�1��+�ޣ�����h��x����0������֤������f��x����������P��b����
��2�����ݵ�һ����գ�x��=x
2-bx+1�����۶Գ�����2�Ĵ�С����b��2ʱ������x��1���գ�x����0������f�䣨x����0���ɵ�f��x�������䣨1��+�ޣ��ϵ����ԣ���b��2ʱ���գ�x��ͼ�����ϣ��Գ��� x=
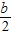
��1����������̦գ�x��=0���������ж������ķ�Χ���Ӷ�ȷ���գ�x���ķ��ţ��õ�f�䣨x���ķ��ţ���������������䣮
��2��������֪������g��x���õ���g�䣨x��=h��x����x
2-2x+1��������h��x����0���������x�ʣ�1��+�ޣ�������
��x��1ʱ��g�䣨x��=h��x����x-1��
2��0���Ӷ�g��x���ڣ�1��+�ޣ��ϵ��������֢�m�ʣ�0��1����m��0��m��1��������������m�÷�Χ����
����⣺��1��f�䣨x��=
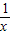
-
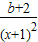
=
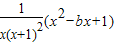
��x��1ʱ��h��x��=
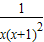
��0�������
�ຯ��f��x����������P��b����
��ii����b��2ʱ������x��1���գ�x��=x
2-bx+1��x
2-2x+1=��x-1��
2��0
����f�䣨x����0���ʴ�ʱf��x�������䣨1��+�ޣ��ϵ�����
��b��2ʱ���գ�x��ͼ�����ϣ��Գ��� x=
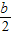
��1��
���̦գ�x��=0������Ϊ��
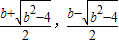
��
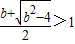
��
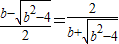
�ʣ�0��1��
�� x�ʣ�1��
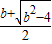
��ʱ���գ�x����0��f�䣨x����0��
�ʴ�ʱf��x�������� ��1��
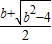
���ϵݼ���
ͬ���ã�f��x��������[
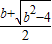
��+�ޣ��ϵ�����
������������b��2ʱ��f��x�������䣨1��+�ޣ��ϵ�����
��b��2ʱ��f��x���� ��1����
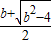
���ϵݼ���f��x����[
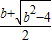
��+�ޣ��ϵ�����
��2��������֪������g��x���õ���g�䣨x��=h��x����x
2-2x+1��������h��x����0���������x�ʣ�1��+�ޣ�������
�൱x��1ʱ��g�䣨x��=h��x����x-1��
2��0���Ӷ�g��x���ڣ�1��+�ޣ��ϵ�������
��m�ʣ�0��1������=mx
1+��1-m��x
2��mx
1+��1-m��x
1=x
1����mx
2+��1-m��x
2=x
2
����ʣ�x
1��x
2��ͬ���ɵæ¡ʣ�x
1��x
2��
��g��x���õ����Կ�֪��g��������g���£��ʣ�g��x
1����g��x
2����
�Ӷ���|g������-g���£�|��|g��x
1��-g��x
2��|��������
��m��0ʱ����=mx
1+��1-m��x
2��mx
2+��1-m��x
2=x
2��=��1-m��x
1+mx
2�ܣ�1-m��x
1+mx
1=mx
1�����ɦ���1���£�1��g��x���õ����Կ�֪g���£���g��x
1����g��x
2����g������
��|g������-g���£�|��|g��x
1��-g��x
2��|�����費��
��m��1ʱ��ͬ���ɵæ���x
1���¡�x
2�������ɵ�|g������-g���£�|��|g��x
1��-g��x
2��|�����費��
�ۺϢ٢ڢۿɵ�m�ʣ�0��1��
������������Ҫ���麯���ĸ�����ʡ�ͼ�����Ȼ���֪ʶ����������������ν�ϡ��������۵�˼�뷽������̽������������������ۺ�������

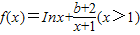 ������bΪʵ����
������bΪʵ����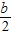 ��1����������̦գ�x��=0���������ж������ķ�Χ���Ӷ�ȷ���գ�x���ķ��ţ��õ�f�䣨x���ķ��ţ���������������䣮
��1����������̦գ�x��=0���������ж������ķ�Χ���Ӷ�ȷ���գ�x���ķ��ţ��õ�f�䣨x���ķ��ţ���������������䣮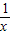 -
-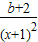 =
=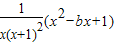
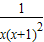 ��0�������
��0�������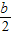 ��1��
��1��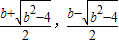
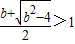 ��
��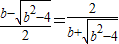 �ʣ�0��1��
�ʣ�0��1��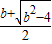 ��ʱ���գ�x����0��f�䣨x����0��
��ʱ���գ�x����0��f�䣨x����0��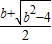 ���ϵݼ���
���ϵݼ���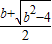 ��+�ޣ��ϵ�����
��+�ޣ��ϵ�����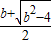 ���ϵݼ���f��x����[
���ϵݼ���f��x����[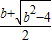 ��+�ޣ��ϵ�����
��+�ޣ��ϵ�����


 ��
�� ��
�� ����
����



