
【题目】在20世纪30年代,地震科学家制定了一种表明地震能量大小的尺度,就是利用测震仪衡量地震的能量等级,等级M与地震的最大振幅A之间满足函数关系M=lgA﹣lgA0 , (其中A0表示标准地震的振幅)
(1)假设在一次4级地震中,测得地震的最大振幅是10,求M关于A的函数解析式;
(2)地震的震级相差虽小,但带来的破坏性很大,计算8级地震的最大振幅是5级地震最大振幅的多少倍.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】【2017庄河高级中学四模】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
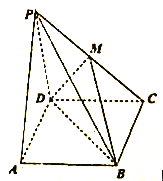
(1)求证: ![]() 平面
平面![]() ;
;
(2)求四面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】样本a1 , a2 , a3 , …,a10的平均数为 ![]() ,样本b1 , b2 , b3 , …,b10的平均数为
,样本b1 , b2 , b3 , …,b10的平均数为 ![]() ,那么样本a1 , b1 , a2 , b2 , …,a10 , b10的平均数为( )
,那么样本a1 , b1 , a2 , b2 , …,a10 , b10的平均数为( )
A.![]() +
+ ![]()
![]()
B.![]() (
( ![]() +
+ ![]() )
)![]()
C.2( ![]() +
+ ![]() )
)
D.![]() (
( ![]() +
+ ![]() )
)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,
, ![]() 、
、![]() 分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线![]() ,使
,使![]() 、
、![]() 关于
关于![]() 的对称点恰好是圆
的对称点恰好是圆![]() :
: ![]()
![]() (
(![]() ,
, ![]() )的一条直径的两个端点.
)的一条直径的两个端点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与抛物线
与抛物线![]() (
(![]() )相交于
)相交于![]() 、
、![]() 两点,射线
两点,射线![]() 、
、![]() 与椭圆
与椭圆![]() 分别相交于点
分别相交于点![]() 、
、![]() .试探究:是否存在数集
.试探究:是否存在数集![]() ,当且仅当
,当且仅当![]() 时,总存在
时,总存在![]() ,使点
,使点![]() 在以线段
在以线段![]() 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据报道,某公司的33名职工的月工资(以元为单位)如下:
职务 | 董事长 | 副董事长 | 董事 | 总经理 | 经理 | 管理员 | 职员 |
人数 | 1 | 1 | 2 | 1 | 5 | 3 | 20 |
工资 | 5 500 | 5 000 | 3 500 | 3 000 | 2 500 | 2 000 | 1 500 |
(1)求该公司职工月工资的平均数、中位数、众数;
(2)假设副董事长的工资从5000元提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数、中位数、众数又是什么?(精确到元)
(3)你认为哪个统计量更能反映这个公司员工的工资水平?结合此问题谈一谈你的看法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解高二年级学生对教师教学的意见,打算从高二年级883名学生中抽取80名进行座谈,若采用下面的方法选取:先用简单随机抽样从883人中剔除3人,剩下880人再按系统抽样的方法进行,则每人入选的概率是( )
A.![]()
B.![]()
C.![]()
D.无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的极坐标方程为
的极坐标方程为![]() .若以极点
.若以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(Ⅰ)求圆![]() 的参数方程;
的参数方程;
(Ⅱ)在直角坐标系中,点![]() 是圆
是圆![]() 上动点,试求
上动点,试求![]() 的最大值,并求出此时点
的最大值,并求出此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知焦点在x轴上的椭圆 ![]() =1(b>0)有一个内含圆x2+y2=
=1(b>0)有一个内含圆x2+y2= ![]() ,该圆的垂直于x轴的切线交椭圆于点M,N,且
,该圆的垂直于x轴的切线交椭圆于点M,N,且 ![]() ⊥
⊥ ![]() (O为原点).
(O为原点). 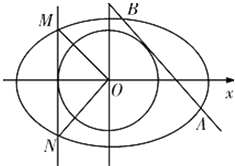
(1)求b的值;
(2)设内含圆的任意切线l交椭圆于点A、B.求证: ![]() ,并求|
,并求| ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017陕西渭南二模】若函数![]() 的图象上存在两个点
的图象上存在两个点![]() 关于原点对称,则对称点
关于原点对称,则对称点![]() 为
为![]() 的“孪生点对”,点对
的“孪生点对”,点对![]() 与
与![]() 可看作同一个“孪生点对”,若函数
可看作同一个“孪生点对”,若函数![]() 恰好有两个“孪生点对”,则实数
恰好有两个“孪生点对”,则实数![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com