练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

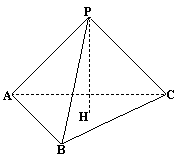
    如图，P为△ABC所在平面外一点，PA⊥PB，PB⊥PC，PC⊥PA，PH⊥平面ABC于H．求证：

    (1)H是△ABC的垂心；

    (2)△ABC为锐角三角形．

    答案：
    解析：

    证明：(1)略．

    (2)由已知，△BPC=90°，PD⊥BC．所以点D在线段BC上．

    又AD⊥BC，从而∠B，∠C都是锐角．同理，∠BAC也是锐角．所以△ABC为锐角三角形．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

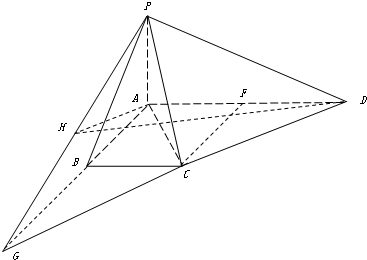    如图，ABCD为直角梯形，∠DAB=∠ABC=90°，AB=BC=1，AD=2，PA⊥平面ABCD，PA=1．
    （1）求点P到CD的距离；
    （2）求证：平面PAC⊥平面PCD；
    （3）求平面PAB与平面PCD所成二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源：2002年高中会考数学必备一本全2002年1月第1版 题型：044

    如图，P为直角三角形ABC所在平面α外一点，∠C＝，PC＝24，P到两条直角边的距离都是6，求：

    　　

    (1)P到平面α的距离；

    (2)PC与平面α所成的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图,点P为斜三棱柱ABC—A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.

           (1)求证:CC1⊥MN;

           (2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF·EF·cos∠DFE.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.

          

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图,点P为斜三棱柱ABC—A1B1C1的侧棱BB1上一点，PM⊥B1B交AA1于点M，PN⊥BB1交CC1于点N.

    (1)求证:CC1⊥MN；

    (2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF·EFcos∠DFE.拓展到空间，类比三角形的余弦定理，写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式，并予以证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    20.如图,点P为斜三棱柱ABC—A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.

     　　 (1)求证：CC1⊥MN；

    　　  (2)在任意△DEF中有余弦定理：

    　　　  DE2＝DF2＋EF2－2DF·EFcosDFE.

    　　  拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面

    积与其中两个侧面所成的二面角之间的关系式,并予以证明.

     

     

    查看答案和解析>>

    同步练习册答案