
【题目】设Sn是数列{an}的前n项和,an>0,且 ![]() .
.
(1)求数列{an}的通项公式;
(2)设 ![]() ,Tn=b1+b2+…+bn , 求证:
,Tn=b1+b2+…+bn , 求证: ![]() .
.
【答案】
(1)解:∵ ![]() ,Sn﹣1=
,Sn﹣1= ![]() an﹣1(an﹣1+3),
an﹣1(an﹣1+3),
∴an= ![]() [
[ ![]() +3an﹣(
+3an﹣( ![]() +3an﹣1)],
+3an﹣1)],
整理得: ![]() ﹣
﹣ ![]() =3(an+an﹣1),
=3(an+an﹣1),
又∵an>0,
∴an﹣an﹣1=3,
又∵a1= ![]() a1(a1+3),即a1=3或a1=0(舍),
a1(a1+3),即a1=3或a1=0(舍),
∴数列{an}是首项、公差均为3的等差数列,
∴其通项公式an=3n
(2)证明:由(1)可知 ![]() =
= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
∴Tn=b1+b2+…+bn
= ![]() (
( ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )
)
= ![]() (
( ![]() ﹣
﹣ ![]() )
)
< ![]()
【解析】(1)通过 ![]() 与Sn﹣1=
与Sn﹣1= ![]() an﹣1(an﹣1+3)作差,进而可知数列{an}是首项、公差均为3的等差数列,计算即得结论;(2)通过(1)裂项可知bn=
an﹣1(an﹣1+3)作差,进而可知数列{an}是首项、公差均为3的等差数列,计算即得结论;(2)通过(1)裂项可知bn= ![]() (
( ![]() ﹣
﹣ ![]() ),进而并项相加即得结论.
),进而并项相加即得结论.
【考点精析】根据题目的已知条件,利用数列的前n项和的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系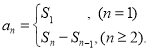 .
.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】双曲线C: ![]() ﹣
﹣ ![]() =1(a>0,b>0)两条渐近线l1 , l2与抛物线y2=﹣4x的准线1围成区域Ω,对于区域Ω(包含边界),对于区域Ω内任意一点(x,y),若
=1(a>0,b>0)两条渐近线l1 , l2与抛物线y2=﹣4x的准线1围成区域Ω,对于区域Ω(包含边界),对于区域Ω内任意一点(x,y),若 ![]() 的最大值小于0,则双曲线C的离心率e的取值范围为 .
的最大值小于0,则双曲线C的离心率e的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x+1|+|x﹣3|
(1)求函数f(x)的最小值;
(2)若{x|f(x)≤t2﹣3t}∩{x|﹣2≤x≤0}≠.求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业常年生产一种出口产品,根据预测可知,进入21世纪以来,该产品的产量平稳增长.记2009年为第1年,且前4年中,第x年与年产量f(x) 万件之间的关系如下表所示:
x | 1 | 2 | 3 | 4 |
f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
若f(x)近似符合以下三种函数模型之一:f(x)=ax+b,f(x)=2x+a,f(x)=log![]() x+a.
x+a.
(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2015年的年产量比预计减少30%,试根据所建立的函数模型,确定2015年的年产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)的定义域是![]() ,对任意
,对任意![]()
当![]() 时,
时,![]() .关于函数
.关于函数![]() 给出下列四个命题:
给出下列四个命题:
①函数![]() 是奇函数;
是奇函数;
②函数![]() 是周期函数;
是周期函数;
③函数![]() 的全部零点为
的全部零点为![]() ;
;
④当![]() 时,函数
时,函数![]() 的图象与函数
的图象与函数![]() 的图象有且只有三个公共点.
的图象有且只有三个公共点.
其中真命题的个数为 .
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代秦九韶算法可计算多项式anxn+an﹣1xn﹣1+…+a1x+a0的值,它所反映的程序框图如图所示,当x=1时,当多项式为x4+4x3+6x2+4x+1的值为( ) 
A.5
B.16
C.15
D.11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com