
分析 (1)依题意得第x年该企业的总利润为(3000+100x)万元,而该企业第x年的人口总数为(2000+ax)人,进而得到答案;
(2)为使该企业的人均利润年年都有增长,则在x>0时,y=f(x)为增函数.进而可得200000-3000a>0,结合实际意义可得答案.
解答 解:(1)依题意得第x年该企业的总利润为(3000+100x)万元,
而该企业第x年的人口总数为(2000+ax)人,
∴y=$\frac{3000+100x}{2000+ax}$…(5分)
(2)为使该企业的人均利润年年都有增长,
则在x>0时,y=f(x)为增函数.
设1≤x1<x2,则f(x1)-f(x2)=$\frac{3000+100{x}_{1}}{2000+a{x}_{1}}$-$\frac{3000+100{x}_{2}}{2000+a{x}_{2}}$=$\frac{(200000-3000a)({x}_{1}-{x}_{2})}{(2000+a{x}_{1})(2000+a{x}_{2})}$<0,…(9分)
∴200000-3000a>0.
∴a<$\frac{200000}{3000}$≈66.7
∴amax=66.
∴该企业每年人口的净增不能超过66人.
点评 本小题主要考查函数模型的选择与应用,属于基础题.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{11}{36}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
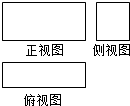 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )| A. | 3$\sqrt{5}$+2 | B. | 6$\sqrt{5}$+4 | C. | 6 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com