
|
| 5 |
| 4 |
| z |
| 40 |
| 5 |
| 4 |
| z |
| 40 |
| 5 |
| 4 |
| z |
| 40 |
| 5 |
| 4 |
| z |
| 40 |
|
|


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
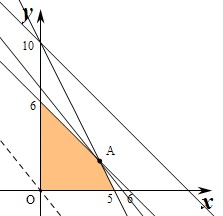
 某服装制造商现有300m2的棉布料,900m2的羊毛料,和600m2的丝绸料.做一条大衣需要1m2的棉布料,5m2的羊毛料,1m2的丝绸料.做一条裤子需要1m2的棉布料,2m2的羊毛料,1m2的丝绸料.
某服装制造商现有300m2的棉布料,900m2的羊毛料,和600m2的丝绸料.做一条大衣需要1m2的棉布料,5m2的羊毛料,1m2的丝绸料.做一条裤子需要1m2的棉布料,2m2的羊毛料,1m2的丝绸料.查看答案和解析>>
科目:高中数学 来源: 题型:044
某服装制造商现有
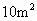 的棉布料,
的棉布料,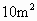 的羊毛料,和
的羊毛料,和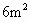 的丝绸料.做一条裤子需要
的丝绸料.做一条裤子需要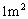 的棉布料,
的棉布料,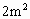 的羊毛料,
的羊毛料,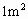 的丝绸料.一条裙子需要
的丝绸料.一条裙子需要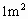 的棉布料,
的棉布料,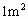 的羊毛料,
的羊毛料,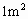 的丝绸料.一条裤子的纯收益是20元,一条裙子的纯收益是40元.为了使收益达到最大,需要安排生产这两种服装的计划,请你列出生产这两种服装件数所要满足的数学关系式,并画出图形.
的丝绸料.一条裤子的纯收益是20元,一条裙子的纯收益是40元.为了使收益达到最大,需要安排生产这两种服装的计划,请你列出生产这两种服装件数所要满足的数学关系式,并画出图形.查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二上学期期中考试理科数学试卷(解析版) 题型:填空题
某服装制造商现有 的棉布料,
的棉布料,  的羊毛料,和
的羊毛料,和 的丝绸料.做一条裤子需要
的丝绸料.做一条裤子需要 的棉布料,
的棉布料,  的羊毛料,
的羊毛料,  的丝绸料.一条裙子需要
的丝绸料.一条裙子需要 的棉布料,
的棉布料,  的羊毛料,
的羊毛料,  的丝绸料.一条裤子的纯收益是50元,一条裙子的纯收益是40元,则该服装制造商的最大收益为
元.
的丝绸料.一条裤子的纯收益是50元,一条裙子的纯收益是40元,则该服装制造商的最大收益为
元.
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二上学期期中考试文科数学试卷(解析版) 题型:填空题
某服装制造商现有 的棉布料,
的棉布料, 的羊毛料,和
的羊毛料,和 的丝绸料.做一条裤子需要
的丝绸料.做一条裤子需要 的棉布料,
的棉布料, 的羊毛料,
的羊毛料, 的丝绸料.一条裙子需要
的丝绸料.一条裙子需要 的棉布料,
的棉布料, 的羊毛料,
的羊毛料,  的丝绸料.一条裤子的纯收益是50元,一条裙子的纯收益是40元,则该服装制造商的最大收益为
元.
的丝绸料.一条裤子的纯收益是50元,一条裙子的纯收益是40元,则该服装制造商的最大收益为
元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com