
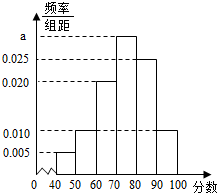
 ��ijУ�����꼶ѧ���г�ȡ40��ѧ���������Ǹ���ѧҵˮƽ���Ե���ѧ�ɼ�������100�֣��ɼ���Ϊ������40�ֵ��������ֳ����Σ�[40��50����[50��60��������[90��100]��õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
��ijУ�����꼶ѧ���г�ȡ40��ѧ���������Ǹ���ѧҵˮƽ���Ե���ѧ�ɼ�������100�֣��ɼ���Ϊ������40�ֵ��������ֳ����Σ�[40��50����[50��60��������[90��100]��õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��

 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A��
| ||||
B��
| ||||
C��
| ||||
D��
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| cosx | ||||
sin4
|
| A��-1 | ||
B��-
| ||
| C��0 | ||
| D��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a |
| 5 |
| b |
| ||
| 5 |
| cos(3��-��) | ||||
sin(
|
sin(
| ||||
cos(3��+��)sin(
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����Ҷͼ��¼�˼ס��������3��ͬѧ����ĩ�����е���ѧ�ɼ������С������ͬѧ�ɼ��ķ���Ϊ
��ͼ����Ҷͼ��¼�˼ס��������3��ͬѧ����ĩ�����е���ѧ�ɼ������С������ͬѧ�ɼ��ķ���Ϊ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| y |
| x |
| (x-2)2+y2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
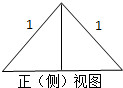 ��ͼ����һ����������ͼ������ͼ���Ͳ���ͼ������ͼ��Ϊ������ȫ��ͬ�ĵ���ֱ�������Σ�������Ϊ1��������������Ϊ��������
��ͼ����һ����������ͼ������ͼ���Ͳ���ͼ������ͼ��Ϊ������ȫ��ͬ�ĵ���ֱ�������Σ�������Ϊ1��������������Ϊ��������A��
| ||||
B��
| ||||
C��
| ||||
D��
|
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com