
分析 (1)根据函数的性质求出集合A,B,结合集合的基本运算进行求解即可.
(2)根据条件A∪C=R,建立条件关系即可.
解答 解:(1)由$\left\{\begin{array}{l}{x-3≥0}\\{7-x>0}\end{array}\right.$得$\left\{\begin{array}{l}{x≥3}\\{x<7}\end{array}\right.$,解得3≤x<7,即A=[3,7).B={y|y=-x2+2x+5=-(x-1)2+6,x∈(-1,2]}=(2,6],
则A∩B=[3,6],A∪B=(2,7),(∁RA)∩B=(2,3);
(2)∵C={x∈R|x<a或x>a+1}.
∴若A∪C=R,则$\left\{\begin{array}{l}{a≥3}\\{a+1<7}\end{array}\right.$,
即$\left\{\begin{array}{l}{a≥3}\\{a<6}\end{array}\right.$,解得3≤a<6,即实数a的取值范围是[3,6).
点评 本题主要考查集合的基本运算,根据函数的性质求出集合A,B是解决本题的关键.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源:2016-2017学年云南大理州南涧县民族中学高二文9月月考数学试卷(解析版) 题型:解答题
设等比数列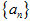 的前
的前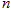 项和为
项和为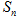 ,已知,
,已知,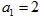 ,且
,且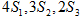 成等差数列.
成等差数列.
(Ⅰ)求数列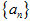 的公比
的公比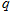 ;
;
(Ⅱ)设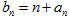 ,求数列
,求数列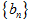 的前
的前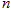 项和
项和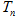 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com