
【题目】已知函数![]() (
(![]() 为自然对数的底数),其中
为自然对数的底数),其中![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(Ⅱ)求![]() 零点的个数.
零点的个数.
【答案】(Ⅰ)函数![]() 的单调增区间是
的单调增区间是![]() ;单调减区间是
;单调减区间是![]() .(Ⅱ)当
.(Ⅱ)当![]() 或
或![]() 时,函数
时,函数![]() 只有一个零点;当
只有一个零点;当![]() 或
或![]() 时,函数
时,函数![]() 有两个零点;当
有两个零点;当![]() 时,函数
时,函数![]() 有三个零点.
有三个零点.
【解析】
(Ⅰ)对函数求导,根据导数的正负即可容易判断函数的单调性;
(Ⅱ)分离参数,构造函数![]() ,利用导数研究函数的单调性,即可容易判断.
,利用导数研究函数的单调性,即可容易判断.
(Ⅰ)当![]() 时,
时,![]() ,故可得
,故可得![]() ,
,
令![]() ,解得
,解得![]() ,
,
故![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增.
单调递增.
(Ⅱ)因为![]()
故当![]() 时,
时,![]() ,即
,即![]() 一定是函数
一定是函数![]() 的一个零点.
的一个零点.
又当![]() 时,令
时,令![]() ,分离参数可得:
,分离参数可得:
![]() ,令
,令![]() ,故可得
,故可得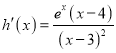 ,
,
令![]() ,解得
,解得![]() ,
,
故![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 和
和![]() 单调递减.
单调递减.
且当![]() 时,
时,![]() ,且当
,且当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,且当
,且当![]() 时,
时,![]() ;
;
又![]() ,故
,故![]() 的图像如下所示:
的图像如下所示:
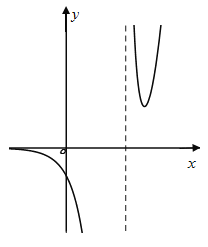
故当![]() ,即
,即![]() 时,
时,![]() 与
与![]() 有一个交点,
有一个交点,
当![]() ,即
,即![]() 时,
时,![]() 与
与![]() 有一个交点,
有一个交点,
当![]() ,即
,即![]() 时,
时,![]() 与
与![]() 有两个交点,
有两个交点,
当![]() ,即可
,即可![]() 时,
时,![]() 与
与![]() 没有交点,
没有交点,
综上所述:当![]() 时,
时,![]() 有3个零点;
有3个零点;
当![]() 时,
时,![]() 有1个零点;
有1个零点;
当![]() 或
或![]() 时,
时,![]() 有2个零点.
有2个零点.


科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面是等腰梯形,
的底面是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为等边三角形,且点P在底面
为等边三角形,且点P在底面![]() 上的射影为
上的射影为![]() 的中点G,点E在线段
的中点G,点E在线段![]() 上,且
上,且![]() .
.
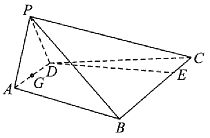
(1)求证:![]() 平面
平面![]() .
.
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区为了了解业主用水情况,该小区分为一期和二期,入住共达4000户,现在通过随机抽样获得了100户居民的月均用水量,下图是调查结果的频数分布表和频率分布直方图.
分组 |
|
|
|
|
|
频数 | 4 | 8 | 15 | 22 | 25 |
分组 |
|
|
|
| |
频数 | 14 | 6 | 4 | 2 |
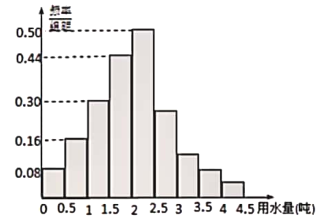
(1)估计该小区月均用水量超过3.8吨约有多少户;(2)通过频率分布直方图,估计该小区居民月均用水量平均值和中位数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),若以O为极点,x轴的正半轴为极轴且取相同的单位长度建立极坐标系,曲线C的极坐标方程为
(t为参数),若以O为极点,x轴的正半轴为极轴且取相同的单位长度建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求曲线C的直角坐标方程及直线l的普通方程;
(2)将所得曲线C向右平移1个单位长度,再将曲线C上的所有点的横坐标变为原来的2倍,得到曲线![]() ,求曲线
,求曲线![]() 上的点到直线l的距离的最大值.
上的点到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线定位法是通过测定待定点到至少三个已知点的两个距离差所进行的一种无线电定位.通过船(待定点)接收到三个发射台的电磁波的时间差计算出距离差,两个距离差即可形成两条位置双曲线,两者相交便可确定船位.我们来看一种简单的“特殊”状况;如图所示,已知三个发射台分别为![]() ,
,![]() ,
,![]() 且刚好三点共线,已知
且刚好三点共线,已知![]() 海里,
海里,![]() 海里,现以
海里,现以![]() 的中点为原点,
的中点为原点,![]() 所在直线为
所在直线为![]() 轴建系.现根据船
轴建系.现根据船![]() 接收到
接收到![]() 点与
点与![]() 点发出的电磁波的时间差计算出距离差,得知船
点发出的电磁波的时间差计算出距离差,得知船![]() 在双曲线
在双曲线![]() 的左支上,根据船
的左支上,根据船![]() 接收到
接收到![]() 台和
台和![]() 台电磁波的时间差,计算出船
台电磁波的时间差,计算出船![]() 到
到![]() 发射台的距离比到
发射台的距离比到![]() 发射台的距离远30海里,则点
发射台的距离远30海里,则点![]() 的坐标(单位:海里)为( )
的坐标(单位:海里)为( )

A. B.
B.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,△ABC是边长为6的等边三角形,D,E分别为AA1,BC的中点.
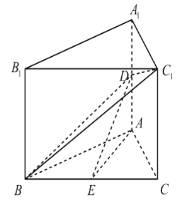
(1)证明:AE//平面BDC1;
(2)若异面直线BC1与AC所成角的余弦值为![]() .求DE与平面BDC1所成角的正弦值.
.求DE与平面BDC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小芳、小明两人各拿两颗质地均匀的骰子做游戏,规则如下:若掷出的点数之和为4的倍数,则由原投掷人继续投掷;若掷出的点数之和不是4的倍数,则由对方接着投掷.
(1)规定第1次从小明开始.
(ⅰ)求前4次投掷中小明恰好投掷2次的概率;
(ⅱ)设游戏的前4次中,小芳投掷的次数为![]() ,求随机变量
,求随机变量![]() 的分布列与期望.
的分布列与期望.
(2)若第1次从小芳开始,求第![]() 次由小芳投掷的概率
次由小芳投掷的概率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张军自主创业,在网上经营一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元千克,为增加销量,张军对这四种干果进行促销:一次购买干果的总价达到150元,顾客就少付x(2x∈Z)元.每笔订单顾客网上支付成功后,张军会得到支付款的80%.
①若顾客一次购买松子和腰果各1千克,需要支付180元,则x=________;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com