【题目】根据下列条件分别求出直线l的方程.
（1）直线l经过A（4，1），且横、纵截距相等；
（2）直线l平行于直线3x+4y+17＝0，并且与两坐标轴围成的三角形的面积为24.
【答案】（1）直线l的方程为：x+y﹣5＝0，或x﹣4y＝0（2）满足条件的直线方程为：3x+4y±24＝0
【解析】
（1）当直线过原点时，方程为
，当直线不过原点时，设直线的方程为：
，把点
代入直线的方程可得
值，即得所求的直线方程
（2）直线与
平行，故可设直线方程为
，求出直线与两坐标轴的交点，即可得到三角形的面积，求出
的值.
（1）直线l经过原点时满足条件，设直线方程为
，
，
因为直线过点
，可得直线方程为：，即
直线l不经过原点时，设直线方程为：，把代入可得：
.
∴直线l的方程为：
.
综上可得：直线l的方程为：或.
（2）设直线l的方程为：，
与坐标轴的交点分别为：
，
.
，解得：
.
∴满足条件的直线方程为：
.
优学名师名题系列答案科目：高中数学 来源： 题型：
【题目】军训时，甲、乙两名同学进行射击比赛，共比赛10场，每场比赛各射击四次，且用每场击中环数之和作为该场比赛的成绩．数学老师将甲、乙两名同学的10场比赛成绩绘成如图所示的茎叶图，并给出下列4个结论：(1)甲的平均成绩比乙的平均成绩高；(2)甲的成绩的极差是29；(3)乙的成绩的众数是21；(4)乙的成绩的中位数是18．则这4个结论中，正确结论的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C： 
，直线l： 
（Ⅰ）求直线l所过定点A的坐标；
（Ⅱ）求直线l被圆C所截得的弦长最短时m的值及最短弦长；
（Ⅲ）已知点
，在直线MC上（C为圆心），存在定点N（异于点M），满足：对于圆C上任一点P，都有
为一常数，试求所有满足条件的点N的坐标及该常数。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“科技引领，布局未来”科技研发是企业发展的驱动力量。
年，某企业连续
年累计研发投入搭
亿元，我们将研发投入与经营投入的比值记为研发投入占营收比，这年间的研发投入（单位：十亿元）用右图中的折现图表示，根据折线图和条形图，下列结论错误的使（ ）
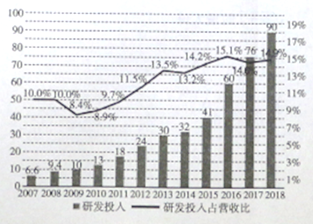
A. 
年至
年研发投入占营收比增量相比
年至
年增量大
B. 年至
年研发投入增量相比
年至
年增量小
C. 该企业连续年研发投入逐年增加
D. 该企业来连续年来研发投入占营收比逐年增加
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在三棱锥P-ABC中，三条侧棱PA、PB、PC两两垂直，且
，
，又M是底面ABC内一点，则M到三个侧面的距离的平方和的最小值是________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线C：
与双曲线
有相同的渐近线，且双曲线C过点
．
(1)若双曲线C的左、右焦点分别为
，
，双曲线C上有一点P，使得
，求△
的面积；
(2)过双曲线C的右焦点作直线l与双曲线右支交于A，B两点，若△
的周长是
，求直线l的方程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
