
【题目】已知正方体ABCD﹣A1B1C1D1中,M,N分别为棱AB,DD1的中点,异面直线A1M和C1N所成的角为( ) 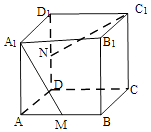
A.30°
B.45°
C.60°
D.90°
科目:高中数学 来源: 题型:
【题目】微信运动和运动手环的普及,增强了人民运动的积极性,每天一万步称为一种健康时尚,某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动,经过几个月的扎实落地工作后,学校想了解全校师生每天一万步的情况,学校界定一人一天走路不足![]() 千步为不健康生活方式,不少于
千步为不健康生活方式,不少于![]() 千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为
千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为![]() 人,高一学生人数为
人,高一学生人数为![]() 人,高二学生人数
人,高二学生人数![]() 人,高三学生人数
人,高三学生人数![]() ,从中抽取
,从中抽取![]() 人作为调查对象,得到了如图所示的这
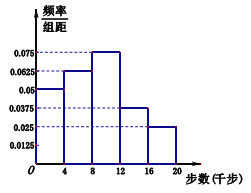
人作为调查对象,得到了如图所示的这![]() 人的频率分布直方图,这
人的频率分布直方图,这![]() 人中有
人中有![]() 人被学校界定为不健康生活方式者.
人被学校界定为不健康生活方式者.
(1)求这次作为抽样调查对象的教师人数;
(2)根据频率分布直方图估算全校师生每人一天走路步数的中位数(四舍五入精确到整数步);
(3)校办公室欲从全校师生中速记抽取![]() 人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励
人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励![]() 元,超健康生活方式者表彰奖励
元,超健康生活方式者表彰奖励![]() 元,一般生活方式者鼓励性奖励
元,一般生活方式者鼓励性奖励![]() 元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为
元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第1组 | [18,28) | 5 | 0.5 |
第2组 | [28,38) | 18 | a |
第3组 | [38,48) | 27 | 0.9 |
第4组 | [48,58) | x | 0.36 |
第5组 | [58,68) | 3 | 0.2 |
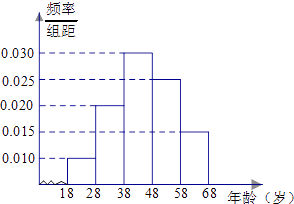
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为加强学生的交通安全教育,对学校旁边![]() ,
,![]() 两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且
两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且![]() 路口数据的平均数比
路口数据的平均数比![]() 路口数据的平均数小2.
路口数据的平均数小2.
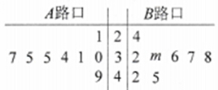
(1)求出![]() 路口8个数据中的中位数和茎叶图中
路口8个数据中的中位数和茎叶图中![]() 的值;
的值;
(2)在![]() 路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的增函数,且对于任意的x都有f(﹣x)+f(x)=0恒成立,如果实数a,b满足不等式组 ![]() ,那么a2+b2的取值范围是( )
,那么a2+b2的取值范围是( )
A.[9,49]
B.(17,49]
C.[9,41]
D.(17,41]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为3 ![]() ,b﹣c=2,cosA=﹣
,b﹣c=2,cosA=﹣ ![]() .
.
(1)求a和sinC的值;
(2)求cos(2A+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,已知对任意n∈N* , a1+a2+a3+…+an=3n﹣1,则a12+a22+a32+…+an2等于( )
A.(3n﹣1)2
B.![]()
C.9n﹣1
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x-3)ex+ax,aR
(1)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程;
(2)当a[0,e)时,设函数f(x)在(1,+)上的最小值为g(a),求函数g(a)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com