
【题目】已知函数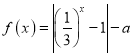 .
.
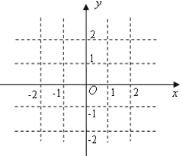
(1)若![]() ,画出函数
,画出函数![]() 的图象,并指出函数的单调区间;
的图象,并指出函数的单调区间;
(2)讨论函数![]() 的零点个数.
的零点个数.
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】定义在R上的函数![]() 和二次函数
和二次函数![]() 满足:
满足:![]() ,
,![]() ,
,![]()
(1)求![]() 和
和![]() 的解析式;
的解析式;
(2)若对于![]() ,
,![]() ,均有
,均有![]() 成立,求a的取值范围;
成立,求a的取值范围;
(3)设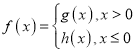 ,在(2)的条件下,讨论方程
,在(2)的条件下,讨论方程![]() 的解的个数.
的解的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的焦点为(![]() ,0),(
,0),(![]() ,0),且椭圆C过点M(4,1),直线l:
,0),且椭圆C过点M(4,1),直线l:![]() 不过点M,且与椭圆交于不同的两点A,B.
不过点M,且与椭圆交于不同的两点A,B.
(1)求椭圆C的标准方程;
(2)求证:直线MA,MB与x轴总围成一个等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() :
:![]() 的焦点,点
的焦点,点![]() 为抛物线
为抛物线![]() 的对称轴与其准线的交点,过
的对称轴与其准线的交点,过![]() 作抛物线
作抛物线![]() 的切线,切点为
的切线,切点为![]() ,若点
,若点![]() 恰好在以
恰好在以![]() ,
,![]() 为焦点的双曲线上,则双曲线的离心率为( )
为焦点的双曲线上,则双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)设![]() 为
为![]() 上的一点,满足
上的一点,满足![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且斜率为
且斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() :
:![]() 交椭圆
交椭圆![]() 于
于![]() 两点.
两点.

(1)求椭圆![]() 的方程;
的方程;
(2)求证:点![]() 在直线
在直线![]() 上;
上;
(3)是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学家门前有一笔直公路直通长城,星期天,他骑自行车匀速前往旅游,他先前进了![]() ,觉得有点累,就休息了一段时间,想想路途遥远,有些泄气,就沿原路返回骑了
,觉得有点累,就休息了一段时间,想想路途遥远,有些泄气,就沿原路返回骑了![]() , 当他记起诗句“不到长城非好汉”,便调转车头继续前进. 则该同学离起点的距离
, 当他记起诗句“不到长城非好汉”,便调转车头继续前进. 则该同学离起点的距离![]() 与时间
与时间![]() 的函数关系的图象大致为( )
的函数关系的图象大致为( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com