
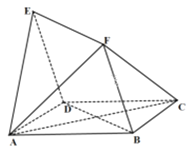
【题目】如图,四边形![]() 与
与![]() 均为菱形,
均为菱形,![]() ,且
,且![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)若![]() 为线段
为线段![]() 上的一点,满足直线
上的一点,满足直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,证明
,证明![]() ,
,![]() 得到答案.
得到答案.
(2)先证明![]() 两两垂直,如图所示建立直角坐标系,分别计算法向量,利用夹角公式得到答案.
两两垂直,如图所示建立直角坐标系,分别计算法向量,利用夹角公式得到答案.
(3)设![]() ,则
,则![]() ,利用夹角公式计算得到答案.
,利用夹角公式计算得到答案.
(1)设![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,
∵四边形![]() 为菱形,∴
为菱形,∴![]() ,且
,且![]() 为
为![]() 中点,∵
中点,∵![]() ,
,
∴![]()
又![]() ,
,![]()
∴![]() 平面
平面![]() .
.
(2)连接![]() ,∵四边形
,∵四边形![]() 为菱形,且
为菱形,且![]() ,
,
∴![]() 为等边三角形,∵
为等边三角形,∵![]() 为
为![]() 中点,∴
中点,∴![]()
又![]() ,
,![]()
∴![]() 平面
平面![]() . ∵
. ∵![]() 两两垂直
两两垂直
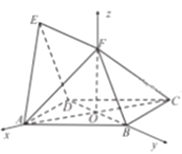
∴建立空间直角坐标系![]() ,如图所示:
,如图所示:
∵四边形![]() 为菱形,
为菱形,![]() ,
, ![]() ,∴
,∴![]() .
.
∵![]() 为等边三角形,∴
为等边三角形,∴![]() .
.
∴![]() ,
,
∴![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则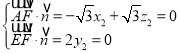
令![]() ,则
,则![]() ,得
,得![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则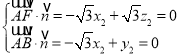 ,
,
令![]() ,则
,则![]() ,得
,得![]()
所以 
又因为二面角![]() 为钝角,
为钝角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(3)设![]()
![]()
则![]()
所以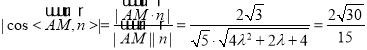
化简得![]()
解得:![]() 或
或![]() (舍) 所以
(舍) 所以![]() .
.


科目:高中数学 来源: 题型:
【题目】若动点![]() 到定点
到定点![]() 与定直线
与定直线![]() 的距离之和为4.
的距离之和为4.
(1)求点![]() 的轨迹方程,并画出方程的曲线草图.
的轨迹方程,并画出方程的曲线草图.
(2)记(1)得到的轨迹为曲线![]() ,若曲线
,若曲线![]() 上恰有三对不同的点关于点
上恰有三对不同的点关于点![]() 对称,求
对称,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网购逐步走入百姓生活,网络(电子)支付方面的股票受到一些股民的青睐.某单位4位热爱炒股的好朋友研究后决定购买“生意宝”和“九州通“这两支股票中的一支.他们约定:每人通过掷一枚质地均匀的骰子决定购买哪支股票,掷出点数为5或6的人买“九州通”股票,掷出点数为小于5的人买“生意宝”股票,且必须从“生意宝”和“九州通”这两支股票中选择一支股票购买.
(1)求这4人中恰有1人购买“九州通”股票的機率;
(2)用![]() ,
,![]() 分别表示这4人中购买“生意宝”和“九州通”股票的人数,记
分别表示这4人中购买“生意宝”和“九州通”股票的人数,记![]() ,求随机变量X的分布列与数学期望
,求随机变量X的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
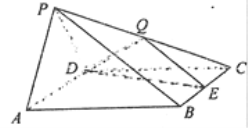
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,侧面
是边长为2的菱形,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上.
上.
(1)求证:![]() ;.
;.
(2)若![]() 是
是![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值;
的余弦值;
(3)若![]() ,当
,当![]() 平面
平面![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处取得最大值,求实数
处取得最大值,求实数![]() 的值;
的值;
(2)若![]() ,求
,求![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)若![]() ,直线
,直线![]() 都不是曲线
都不是曲线![]() 的切线,求
的切线,求![]() 的取值范围(只需直接写出结果).
的取值范围(只需直接写出结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
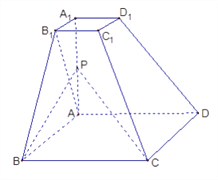
【题目】已知四棱台![]() 的上下底面分别是边长为2和4的正方形,
的上下底面分别是边长为2和4的正方形, ![]() = 4且
= 4且 ![]() ⊥底面
⊥底面![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 面
面 ![]() ;
;
(Ⅱ)在![]() 边上找一点
边上找一点![]() ,使
,使![]() ∥面
∥面![]() ,
,
并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com