
【题目】2020年寒假期间新冠肺炎肆虐,全国人民众志成城抗击疫情.某市要求全体市民在家隔离,同时决定全市所有学校推迟开学.某区教育局为了让学生“停课不停学”,要求学校各科老师每天在网上授课,每天共280分钟,请学生自主学习.区教育局为了了解高三学生网上学习情况,上课几天后在全区高三学生中采取随机抽样的方法抽取了100名学生进行问卷调查,为了方便表述把学习时间在![]() 分钟的学生称为
分钟的学生称为![]() 类,把学习时间在
类,把学习时间在![]() 分钟的学生称为
分钟的学生称为![]() 类,把学习时间在
类,把学习时间在![]() 分钟的学生称为
分钟的学生称为![]() 类,随机调查的100名学生学习时间的人数频率分布直方图如图所示:以频率估计概率回答下列问题:
类,随机调查的100名学生学习时间的人数频率分布直方图如图所示:以频率估计概率回答下列问题:

(1)求100名学生中![]() ,
,![]() ,
,![]() 三类学生分别有多少人?
三类学生分别有多少人?
(2)在![]() ,
,![]() ,
,![]() 三类学生中,按分层抽样的方法从上述100个学生中抽取10人,并在这10人中任意邀请3人电话访谈,求邀请的3人中是
三类学生中,按分层抽样的方法从上述100个学生中抽取10人,并在这10人中任意邀请3人电话访谈,求邀请的3人中是![]() 类的学生人数的分布列和数学期望;
类的学生人数的分布列和数学期望;
(3)某校高三(1)班有50名学生,某天语文和数学老师计划分别在19:00—19:40和20:00—20:40在线上与学生交流,由于受校园网络平台的限制,每次只能30个人同时在线学习交流.假设这两个时间段高三(1)班都有30名学生相互独立地随机登录参加学习交流.设![]() 表示参加语文或数学学习交流的人数,当
表示参加语文或数学学习交流的人数,当![]() 为多少时,其概率最大.
为多少时,其概率最大.
【答案】(1)30;(2)分布列见解析,![]() ;(3)42.
;(3)42.
【解析】
(1)根据频率分布直方图即可求出结果;
(2)根据分层抽样可知从![]() 类中抽2人,
类中抽2人,![]() 类中抽5人,
类中抽5人,![]() 类中抽3人,再根据超几何分布列出分布列,求出期望;
类中抽3人,再根据超几何分布列出分布列,求出期望;
(3)学生随机独立参加语文或数学在线辅导所包含的基本事件总数为![]() ,当
,当![]() 时,由韦恩图可知,事件
时,由韦恩图可知,事件![]() 所包含的基本事件的总数为
所包含的基本事件的总数为![]() ,
,
所以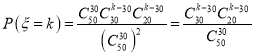 最大,列出不等式组,可得
最大,列出不等式组,可得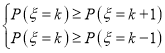 ,由此即可求出结果.
,由此即可求出结果.
(1)![]() 类学生有:
类学生有:![]() 人,
人,
![]() 类学生有:
类学生有:![]() 人,
人,
![]() 类学生有:
类学生有:![]() 人.
人.
(2)![]() ,
,
故从![]() 类中抽2人,
类中抽2人,![]() 类中抽5人,
类中抽5人,![]() 类中抽3人.
类中抽3人.
设邀请的三人中是![]() 类的学生人数为
类的学生人数为![]() ,则
,则![]() 可取0,1,2,3.
可取0,1,2,3.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() .
.
(3)学生随机独立参加语文或数学在线辅导所包含的基本事件总数为![]() ,
,
当![]() 时,由韦恩图可知,只参加语文辅导的人数为
时,由韦恩图可知,只参加语文辅导的人数为![]() ,
,
只参加数学辅导的人数为![]() ,
,
语文和数学都参加辅导的人数为![]() .
.
事件![]() 所包含的基本事件的总数为
所包含的基本事件的总数为![]() ,
,
所以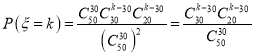 最大.
最大.
则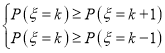 ,
,
所以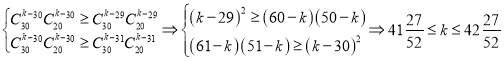 .
.
又因为![]() ,所以
,所以![]() .
.



科目:高中数学 来源: 题型:
【题目】Keep是一款具有社交属性的健身APP,致力于提供健身教学跑步骑行交友及健身饮食指导装备购买等--站式运动解决方案.Keep可以让你随时随地进行锻炼,记录你每天的训练进程不仅如此,它还可以根据不同人的体质,制定不同的健身计划小吴根据Keep记录的2019年1月至2019年11月期间每月跑步的里程(单位:十公里)数据整理并绘制了下面的折线图根据该折线图,下列结论正确的是( ).

A.月跑步里程逐月增加
B.月跑步里程最大值出现在10月
C.月跑步里程的中位数为5月份对应的里程数
D.1月至5月的月跑步里程相对于6月至11月波动性更小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某快递公司收取快递费的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,在收费
的包裹,在收费![]() 元的基础上,每超过
元的基础上,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该快递公司承揽了一个工艺品厂家的全部玻璃工艺品包裹的邮寄事宜,该厂家随机统计了
元.该快递公司承揽了一个工艺品厂家的全部玻璃工艺品包裹的邮寄事宜,该厂家随机统计了![]() 件这种包裹的两个统计数表如下:
件这种包裹的两个统计数表如下:
表![]()
包裹重量 |
|
|
|
|
|
包裹数 |
|
|
|
|
|
损坏件数 |
|
|
|
|
|
表![]()
包裹重量 |
|
|
|
|
|
出厂价(元 |
|
|
|
|
|
卖价(元 |
|
|
|
|
|
![]() 估计该快递公司对每件包裹收取快递费的平均值;
估计该快递公司对每件包裹收取快递费的平均值;
![]() 将包裹重量落入各组的频率视为概率,该工艺品厂家承担全部运费,每个包裹只有一件产品,如果客户收到有损坏品的包裹,该快递公司每件按其出厂价的
将包裹重量落入各组的频率视为概率,该工艺品厂家承担全部运费,每个包裹只有一件产品,如果客户收到有损坏品的包裹,该快递公司每件按其出厂价的![]() 赔偿给厂家.现该厂准备给客户邮寄重量在区间
赔偿给厂家.现该厂准备给客户邮寄重量在区间![]() 和
和![]() 内的工艺品各
内的工艺品各![]() 件,求该厂家这两件工艺品获得利润的分布列和期望.
件,求该厂家这两件工艺品获得利润的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是离心率为
分别是离心率为![]() 的椭圆
的椭圆![]() 的左、右顶点,
的左、右顶点,![]() 是椭圆
是椭圆![]() 的右焦点,且
的右焦点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() .
.
①若![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 横坐标的取值范围;
横坐标的取值范围;
②设直线![]() 交直线
交直线![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某外国语学校举行的![]() (高中生数学建模大赛)中,参与大赛的女生与男生人数之比为
(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖.按女生、男生用分层抽样的方法抽取
)的同学获奖.按女生、男生用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图如图所示.
人的成绩作为样本,得到成绩的频率分布直方图如图所示.
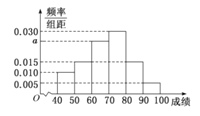
(Ⅰ)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)填写下面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下能否认为“获奖与女生、男生有关”.
的前提下能否认为“获奖与女生、男生有关”.
女生 | 男生 | 总计 | |
获奖 |
| ||
不获奖 | |||
总计 |
| ||
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中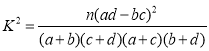 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,并解答.已知等差数列
这三个条件中任选一个,补充在下面问题中,并解答.已知等差数列![]() 的公差
的公差![]() ,前
,前![]() 项和为
项和为![]() ,若_______,数列
,若_______,数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)求![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于给定的数列![]() ,
,![]() ,设
,设![]() ,即
,即![]() 是
是![]() ,
,![]() ,…,
,…,![]() 中的最大值,则称数列
中的最大值,则称数列![]() 是数列
是数列![]() ,
,![]() 的“和谐数列”.
的“和谐数列”.
(1)设![]() ,
,![]() ,求
,求![]() ,
,![]() ,
,![]() 的值,并证明数列
的值,并证明数列![]() 是等差数列;
是等差数列;
(2)设数列![]() ,
,![]() 都是公比为q的正项等比数列,若数列
都是公比为q的正项等比数列,若数列![]() 是等差数列,求公比q的取值范围;
是等差数列,求公比q的取值范围;
(3)设数列![]() 满足
满足![]() ,数列
,数列![]() 是数列
是数列![]() ,
,![]() 的“和谐数列”,且
的“和谐数列”,且![]() (m为常数,
(m为常数,![]() ,2,…,k),求证:
,2,…,k),求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com