
分析 (1)设片集甲、乙分别播放x,y集,则有$\left\{\begin{array}{l}{x+y≥6}\\{20x+8y≤80}\\{x,y∈{N}^{+}}\end{array}\right.$,要使收视观众最多,则只要z=60x+20y最大即可.
(2)由题意得:2a+5b=3,则$\frac{1}{3}$(2a+5b)=1,利用“1”的代换,结合基本不等式,求效益调和指数的最小值.
解答 解:(Ⅰ)设片集甲乙分别播放x,y集,由题意得到$\left\{\begin{array}{l}{x+y≥6}\\{20x+8y≤80}\\{x,y∈{N}^{+}}\end{array}\right.$,要使收视观众最多,只要z=60x+20y最大即可,
作出可行域,如图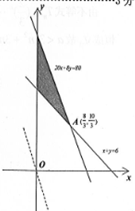
由$\left\{\begin{array}{l}{x+y=6}\\{20x+8y=80}\end{array}\right.$解得A($\frac{8}{3},\frac{10}{3}$),所以满足题意的最优解为(2,5),
zmax=60×2+20×5=220,故电视台每周片集甲播出2集,片集乙每周播出5集,其收视观众最多;
(Ⅱ)由题意得:2a+5b=3,则
S=$\frac{8}{a}+\frac{5}{b}=\frac{1}{3}(2a+5b)(\frac{8}{a}+\frac{5}{b})$=$\frac{1}{3}(41+\frac{40b}{a}+\frac{10a}{b})$≥27,
当且仅当a=$\frac{2}{3}$,b=$\frac{1}{3}$时取等号,所以效益调和指数的最小值为27万元.
点评 本题主要考查了用平面区域二元一次不等式组,考查基本不等式的运用,以及简单的转化思想和数形结合的思想,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰直角三角形 | B. | 等腰钝角三角形 | ||
| C. | 等边三角形 | D. | 不存在这样的三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
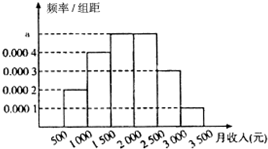 统计局就某地居民的月收入情况调查了10000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在[500,1000).
统计局就某地居民的月收入情况调查了10000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在[500,1000).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com