
| 1 |
| 4 |
| 7 |
| 16 |
| C | 1 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 16 |
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 8 |
| 7 |
| 16 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| 3 |
| C | 1 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 48 |
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 3 |
| 8 |
| 7 |
| 16 |
| 1 |
| 6 |
| 1 |
| 48 |
| 5 |
| 6 |


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 12 |
| 32 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省黄山市七校高三(上)联考数学试卷(理科)(解析版) 题型:解答题
 ;汽车走路②堵车的概率为p.若现在有两辆汽车走路①,有一辆汽车走路②,且这三辆车是否堵车相互之间没有影响.
;汽车走路②堵车的概率为p.若现在有两辆汽车走路①,有一辆汽车走路②,且这三辆车是否堵车相互之间没有影响. ,求走公路②堵车的概率;
,求走公路②堵车的概率;查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省黄山市七校高三(上)联考数学试卷(理科)(解析版) 题型:解答题
 ;汽车走路②堵车的概率为p.若现在有两辆汽车走路①,有一辆汽车走路②,且这三辆车是否堵车相互之间没有影响.
;汽车走路②堵车的概率为p.若现在有两辆汽车走路①,有一辆汽车走路②,且这三辆车是否堵车相互之间没有影响.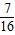 ,求走公路②堵车的概率;
,求走公路②堵车的概率;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com