练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

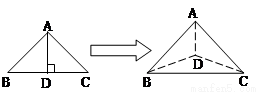
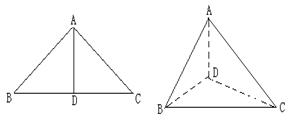
    如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，某学生得出下列四个结论：

    ①；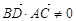

    ②∠BAC＝60°；

    ③三棱锥D—ABC是正三棱锥；

    ④平面ADC的法向量和平面ABC的法向量互相垂直.

    其中正确的是________(填上正确答案的序号)

     

     

     

    【答案】

    ②③

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，某学生得出下列四个结论：
    ①
    BD
    •
    AC
    ≠0    ；
    ②∠BAC=60°；
    ③三棱锥D-ABC是正三棱锥；
    ④平面ADC的法向量和平面ABC的法向量互相垂直．
    其中正确的是（　　）
    A、①②B、②③C、③④D、①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD与△ACD折成互相垂直的两个平面后，某学生得出下列四个结论：
    ①
    BD
    •
    AC
    ≠0    ；
    ②∠BAC=60°；
    ③三棱锥D-ABC是正三棱锥；
    ④平面ADC的法向量和平面ABC的法向量互相垂直．
    其中正确结论的序号是
    ②③
    ②③
    ．（请把正确结论的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，某学生得出下列四个结论：

           ①；

           ②∠BAC＝60°；

           ③三棱锥D—ABC是正三棱锥；

           ④平面ADC的法向量和平面ABC的法向量互相垂直.

           其中正确的是                                                    （    ）

           A．①②          B．②③              C．③④            D．①④

    查看答案和解析>>

    科目：高中数学 来源：2013届辽宁省开原市高二第三次月考理科数学 题型：选择题

    如图，以等腰直角三角形ABC的斜边BC上的高AD为折痕，将ΔABD和ΔACD折起，使折起后的ΔABC成等边三角形，则二面角C-AB-D的余弦值等于             （    ）

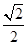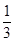    A．            B．      C．              D．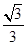

     

     

     

     

    查看答案和解析>>

    同步练习册答案