
【题目】有编号为1,2,3…n的n个学生,入座编号为1,2,3…n的n个座位,每个学生规定坐一个座位, 设学生所坐的座位号与该生的编号不同的学生人数为![]() , 已知
, 已知![]() 时, 共有6种坐法.
时, 共有6种坐法.
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的概率分布列及数学期望
的概率分布列及数学期望![]() .
.
【答案】(1)![]() ;(2)分布列详见解析,
;(2)分布列详见解析,![]() .
.
【解析】
试题(1)解题的关键是ξ=2时,共有6种坐法,写出关于n的表示式,解出未知量,把不合题意的舍去.
(2)学生所坐的座位号与该生的编号不同的学生人数为ξ,由题意知ξ的可能取值是0,2,3,4,当变量是0时表示学生所坐的座位号与该生的编号都相同,当变量是2时表示学生所坐的座位号与该生的编号有2个相同,理解变量对应的事件,写出分布列和期望.
解:(1)∵当ξ=2时,有Cn2种坐法,
∴Cn2=6,
即![]() ,
,
n2﹣n﹣12=0,n=4或n=﹣3(舍去),
∴n=4.
(2)∵学生所坐的座位号与该生的编号不同的学生人数为ξ,
由题意知ξ的可能取值是0,2,3,4,
当变量是0时表示学生所坐的座位号与该生的编号都相同,
当变量是2时表示学生所坐的座位号与该生的编号有2个相同,
当变量是3时表示学生所坐的座位号与该生的编号有1个相同,
当变量是4时表示学生所坐的座位号与该生的编号有0个相同,
∴![]() ,
,
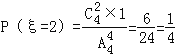 ,
,
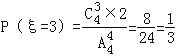 ,
,
![]() ,
,
∴ξ的概率分布列为:
ξ | 0 | 2 | 3 | 4 |
P |
|
|
|
|
∴![]() .
.


科目:高中数学 来源: 题型:
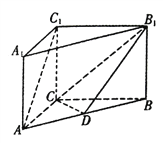
【题目】直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 上的动点.
上的动点.
(1)当点![]() 是
是![]() 的中点时,求证:
的中点时,求证: ![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,试求出
?若存在,试求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述中正确的是( )
A. 若![]() ,则“
,则“![]() ”的充要条件是“
”的充要条件是“![]() ”
”
B. 函数![]() 的最大值是
的最大值是![]()
C. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
D. ![]() 是一条直线,
是一条直线,![]() 是两个不同的平面,若
是两个不同的平面,若![]() 则
则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查高一学生在分班选科时是否选择物理科目与性别的关系,随机调查100名高一学生,得到![]() 列联表如下:由此得出的正确结论是( )
列联表如下:由此得出的正确结论是( )
选择物理 | 不选择物理 | 总计 | |
男 | 35 | 20 | 55 |
女 | 15 | 30 | 45 |
总计 | 50 | 50 | 100 |
附: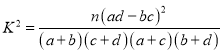
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A.在犯错误的概率不超过0.01的前提下,认为“选择物理与性别有关”
B.在犯错误的概率不超过0.01的前提下,认为“选择物理与性别无关”
C.有![]() 的把握认为“选择物理与性别有关”
的把握认为“选择物理与性别有关”
D.有![]() 的把握认为“选择物理与性别无关”
的把握认为“选择物理与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元,为了增加企业竞争力,决定优化产业结构,调整出x(x∈N*)名员工从事第三产业,调整后他们平均每人每年创造利润为10(a﹣0.8x%)万元(a>0),剩下的员工平均每人每年创造的利润可以提高0.4x%.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创遣的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的“局部对称点”.
的“局部对称点”.
(1)![]() ,其中
,其中![]() ,试判断
,试判断![]() 是否有“局部对称点”?若有,请求出该点;若没有,请说明理由;
是否有“局部对称点”?若有,请求出该点;若没有,请说明理由;
(2)若函数![]() 在区间
在区间![]() 内有“局部对称点”,求实数m的取值范围;
内有“局部对称点”,求实数m的取值范围;
(3)若函数![]() 在R上有“局部对称点”,求实数m的取值范围.
在R上有“局部对称点”,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com