
【题目】已知函数f(x)=|3x-1|-2|x|+2.
(Ⅰ)解不等式:f(x)<10;
(Ⅱ)若对任意的实数x,f(x)-|x|≤a恒成立,求实数a的取值范围.
【答案】(Ⅰ)(-7,9)(Ⅱ)[3,+∞).
【解析】试题分析:(Ⅰ) 对![]() 分三种情况讨论,分别求解不等式组,然后求并集,即可得不等式
分三种情况讨论,分别求解不等式组,然后求并集,即可得不等式![]() 的解集;(Ⅱ)对任意的实数
的解集;(Ⅱ)对任意的实数![]() 恒成立,等价于
恒成立,等价于![]() ,利用
,利用![]() ,可得
,可得![]() ,从而可求实数
,从而可求实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)当x<0时,不等式可化为-(3x-1)-(-2x)+2<10,解得x>-7.所以-7<x<0;
当0≤x≤![]() 时,不等式可化为-(3x-1)-2x+2<10,解得x>-
时,不等式可化为-(3x-1)-2x+2<10,解得x>-![]() .所以0≤x≤
.所以0≤x≤![]() ;
;
当x>![]() 时,不等式可化为(3x-1)-2x+2<10,解得x<9.所以
时,不等式可化为(3x-1)-2x+2<10,解得x<9.所以![]() <x<9.
<x<9.
综上,不等式的解集为(-7,9).
(Ⅱ)f(x)-|x|≤a即为|3x-1|-2|x|+2-|x|≤a,即|3x-1|-3|x|≤a-2.
即|3x-1|-|3x|≤a-2.
因为|3x-1|-|3x|≤|3x-1-3x|=1
所以要对任意的实数x,使得f(x)-2|x|≤a,需使1≤a-2,解得a≥3.
即实数a的取值范围是[3,+∞).


科目:高中数学 来源: 题型:
【题目】如图,一张纸的长、宽分别为2![]() a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是________(写出所有正确命题的序号).
a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是________(写出所有正确命题的序号).

①该多面体是三棱锥;②平面BAD⊥平面BCD;
③平面BAC⊥平面ACD;④该多面体外接球的表面积为5πa2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,AD=CD.
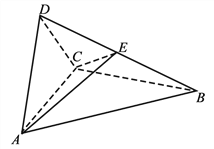
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公比为q的等比数列{an}中,已知a1=16,且a1,a2+2,a3成等差数列.
(Ⅰ)求q,an;
(Ⅱ)若q<1,求满足a1-a2+a3-…+(-1)2n-1a2n>10的最小的正整数n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.

(Ⅰ)求图中实数a,b的值;
(Ⅱ)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于80分的人数;
(Ⅲ)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】家政服务公司根据用户满意程度将本公司家政服务员分为两类,其中A类服务员12名,B类服务员x名.
(Ⅰ)若采用分层抽样的方法随机抽取20名家政服务员参加技术培训,抽取到B类服务员的人数是16, 求x的值;
(Ⅱ)某客户来公司聘请2名家政服务员,但是由于公司人员安排已经接近饱和,只有3名A类家政服务员和2名B类家政服务员可供选择,求该客户最终聘请的家政服务员中既有A类又有B类的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中的假命题是( )
A. α,β∈R,使sin(α+β)=sinα+sinβ
B. φ∈R,函数f(x)=sin(2x+φ)都不是偶函数
C. x0∈R,使![]() (a,b,c∈R且为常数)
(a,b,c∈R且为常数)
D. a>0,函数f(x)=ln2x+lnx-a有零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,∠DAB=60°.
(1)求证:直线AM∥平面PNC;
(2)求二面角D﹣PC﹣N的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com