
【题目】某网络商城在![]() 年
年![]() 月
月![]() 日开展“庆元旦”活动,当天各店铺销售额破十亿,为了提高各店铺销售的积极性,采用摇号抽奖的方式,抽取了
日开展“庆元旦”活动,当天各店铺销售额破十亿,为了提高各店铺销售的积极性,采用摇号抽奖的方式,抽取了![]() 家店铺进行红包奖励.如图是抽取的
家店铺进行红包奖励.如图是抽取的![]() 家店铺元旦当天的销售额(单位:千元)的频率分布直方图.
家店铺元旦当天的销售额(单位:千元)的频率分布直方图.
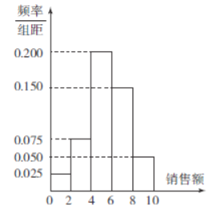
(1)求抽取的这![]() 家店铺,元旦当天销售额的平均值;
家店铺,元旦当天销售额的平均值;
(2)估计抽取的![]() 家店铺中元旦当天销售额不低于
家店铺中元旦当天销售额不低于![]() 元的有多少家;
元的有多少家;
(3)为了了解抽取的各店铺的销售方案,销售额在![]() 和
和![]() 的店铺中共抽取两家店铺进行销售研究,求抽取的店铺销售额在
的店铺中共抽取两家店铺进行销售研究,求抽取的店铺销售额在![]() 和
和![]() 各一个的概率.
各一个的概率.
【答案】(1)![]() 元;(2)32家;(3)
元;(2)32家;(3)![]()
【解析】
(1)频率分布直方图中每个小矩形底边的中点作为该组数据的代表,求出平均数;
(2)在频率分布直方图中找到销售额不低于4000的3个小矩形,算出概率,由此估计40家中有多少家销售额不低于4000;
(3)本题为古典概型,将销售额在![]() 的2家店铺和销售额在
的2家店铺和销售额在![]() 的4家店铺分别编号,用列举法求概率.
的4家店铺分别编号,用列举法求概率.
解:(1)频率分布直方图销售额的平均值为
![]() 千元,
千元,
所以销售额的平均值为![]() 元;
元;
(2)不低于![]() 元的有
元的有![]() 家;
家;
(3)销售额在![]() 的店铺有
的店铺有![]() 家,编号为
家,编号为![]() ,
,![]() ;
;
销售额在![]() 的店铺有
的店铺有![]() 家,编号为
家,编号为![]() ,
,![]() ,
,![]() ,
,![]() .选取两家,
.选取两家,
共有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
![]() 分选取方式,
分选取方式,
其中满足条件的有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 共
共![]() 种,
种,
所以选取的两人销售额在![]() 和
和![]() 各一个的概率为
各一个的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在明代珠算发明之前,我们的先祖从春秋开始多是用算筹为工具来记数、列式和计算.算筹实际上是一根根相同长度的小木棍,如图,是利用算筹表示数1~9的一种方法,例如:47可以表示为“![]() ”,如果用算筹表示一个不含“0”且没有重复数字的三位数,这个数至少要用8根小木棍的概率为( )
”,如果用算筹表示一个不含“0”且没有重复数字的三位数,这个数至少要用8根小木棍的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公园有三条观光大道![]() 围成直角三角形,其中直角边
围成直角三角形,其中直角边![]() ,斜边
,斜边![]() .现有甲、乙、丙三位小朋友分别在
.现有甲、乙、丙三位小朋友分别在![]() 大道上嬉戏,
大道上嬉戏,
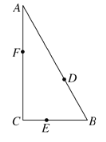
(1)若甲、乙都以每分钟100![]() 的速度从点
的速度从点![]() 出发在各自的大道上奔走,乙比甲迟2分钟出发,当乙出发1分钟后到达
出发在各自的大道上奔走,乙比甲迟2分钟出发,当乙出发1分钟后到达![]() ,甲到达
,甲到达![]() ,求此时甲、乙两人之间的距离;
,求此时甲、乙两人之间的距离;
(2)甲、乙、丙所在位置分别记为点![]() .设
.设![]() ,乙、丙之间的距离是甲、乙之间距离的2倍,且
,乙、丙之间的距离是甲、乙之间距离的2倍,且![]() ,请将甲、乙之间的距离
,请将甲、乙之间的距离![]() 表示为
表示为![]() 的函数,并求甲、乙之间的最小距离.
的函数,并求甲、乙之间的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 焦点为
焦点为![]() ,过点
,过点![]() 与
与![]() 轴垂直的直线交抛物线的弦长为2.
轴垂直的直线交抛物线的弦长为2.
(1)求抛物线![]() 的方程;
的方程;
(2)点![]() 和点
和点![]() 为两定点,点
为两定点,点![]() 和点
和点![]() 为抛物线
为抛物线![]() 上的两动点,线段
上的两动点,线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,求
上,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (
(![]() )的离心率为
)的离心率为![]() ,且短轴的一个端点B与两焦点A,C组成的三角形面积为
,且短轴的一个端点B与两焦点A,C组成的三角形面积为![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)若点P为椭圆E上的一点,过点P作椭圆E的切线交圆O:![]() 于不同的两点M,N(其中M在N的右侧),求四边形
于不同的两点M,N(其中M在N的右侧),求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园有一块边长为3百米的正三角形![]() 空地,拟将它分割成面积相等的三个区域,用来种植三种花卉.方案是:先建造一条直道
空地,拟将它分割成面积相等的三个区域,用来种植三种花卉.方案是:先建造一条直道![]() 将
将![]() 分成面积之比为
分成面积之比为![]() 的两部分(点D,E分别在边
的两部分(点D,E分别在边![]() ,
,![]() 上);再取
上);再取![]() 的中点M,建造直道
的中点M,建造直道![]() (如图).设
(如图).设![]() ,
,![]() ,
,![]() (单位:百米).
(单位:百米).
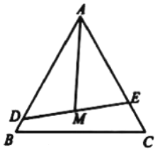
(1)分别求![]() ,
,![]() 关于x的函数关系式;
关于x的函数关系式;
(2)试确定点D的位置,使两条直道的长度之和最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇迹之一,其中较为著名的是胡夫金字塔.令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿,还有发生在胡夫金字塔上的数字“巧合”.如胡夫金字塔的底部周长如果除以其高度的两倍,得到的商为3.14159,这就是圆周率较为精确的近似值.金字塔底部形为正方形,整个塔形为正四棱锥,经古代能工巧匠建设完成后,底座边长大约230米.因年久风化,顶端剥落10米,则胡夫金字塔现高大约为( )
A.128.5米B.132.5米C.136.5米D.110.5米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
,![]() .
.
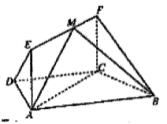
(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,当点
上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com