
【题目】已知数列{an}的前n项和为Sn , 且满足an+2SnSn﹣1=0(n≥2),a1= ![]() .
.
(1)求证:{ ![]() }是等差数列;
}是等差数列;
(2)求an的表达式.
【答案】
(1)证明:∵﹣an=2SnSn﹣1,
∴﹣Sn+Sn﹣1=2SnSn﹣1(n≥2),Sn≠0(n=1,2,3).
∴ ![]() ﹣
﹣ ![]() =2.
=2.
又 ![]() =
= ![]() =2,∴{
=2,∴{ ![]() }是以2为首项,2为公差的等差数列
}是以2为首项,2为公差的等差数列
(2)解:由(1), ![]() =2+(n﹣1)2=2n,∴Sn=
=2+(n﹣1)2=2n,∴Sn= ![]() .
.
当n≥2时,an=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() 〔或n≥2时,an=﹣2SnSn﹣1=﹣
〔或n≥2时,an=﹣2SnSn﹣1=﹣ ![]() 〕;
〕;
当n=1时,S1=a1= ![]() .
.
∴an= 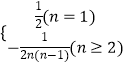
【解析】(1)本题关键是将an=Sn﹣Sn﹣1代入化简,再根据等差数列的定义进行判定即可.(2)先求出Sn , 利用Sn求an , 必须分类讨论an= ![]() ,求解可得.
,求解可得.
【考点精析】利用等差关系的确定和数列的通项公式对题目进行判断即可得到答案,需要熟知如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
)那么这个数列就叫做等差数列;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】某公司过去五个月的广告费支出x与销售额y(单位:万元)之间有下列对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y |
| 40 | 60 | 50 | 70 |
工作人员不慎将表格中y的第一个数据丢失.已知y对x呈线性相关关系,且回归方程为 ![]() =6.5x+17.5,则下列说法:
=6.5x+17.5,则下列说法:
①销售额y与广告费支出x正相关;
②丢失的数据(表中 ![]() 处)为30;
处)为30;
③该公司广告费支出每增加1万元,销售额一定增加6.5万元;
④若该公司下月广告投入8万元,则销售额为70万元.
其中,正确说法有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为14分)如图1所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4.如图2所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连结AB,设点F是AB的中点.

(1)求证:DE⊥平面BCD;
(2)在图2中,若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥BDEG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点,焦点在x轴上的椭圆,离心率为 ![]() 且过点(
且过点( ![]() ,0),过定点C(﹣1,0)的动直线与该椭圆相交于A、B两点.
,0),过定点C(﹣1,0)的动直线与该椭圆相交于A、B两点.
(1)若线段AB中点的横坐标是﹣ ![]() ,求直线AB的方程;
,求直线AB的方程;
(2)在x轴上是否存在点M,使 ![]() 为常数?若存在,求出点M的坐标;若不存在,请说明理由.
为常数?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
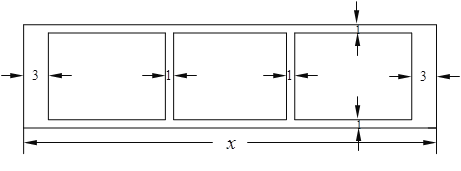
【题目】(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为![]() (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为![]() (m2).
(m2).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于三角形满足的条件,下列判断正确的是( )
A.a=7,b=14,A=30°,有两解
B.a=30,b=25,A=150°,有一解
C.a=6,b=9,A=45°,有两解
D.b=9,c=10,B=60°,无解
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+2ax﹣b2+4
(1)若a是从0,1,2三个数中任取的一个数,b是从﹣2,﹣1,0,1,2五个数中任取的一个数,求函数f(x)有零点的概率;
(2)若a是从区间[﹣3,3]上任取的一个数,b是从区间[0,3]上任取的一个数,求函数g(x)=f(x)+5无零点的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)+1(0≤φ≤ ![]() )的图象相邻两对称轴之间的距离为π,且在x=
)的图象相邻两对称轴之间的距离为π,且在x= ![]() 时取得最大值2.
时取得最大值2.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间;
(3)当f(α)= ![]() ,且
,且 ![]() <α<
<α< ![]() ,求sinα的值.
,求sinα的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com