
【题目】如图,在四棱锥P﹣ABCD中, ![]() 平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形,
平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形, ![]() .
. 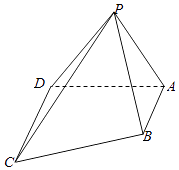
(1)证明:平面PAB⊥平面PCD;
(2)若三棱锥B﹣PAD的体积为 ![]() ,求平面PAD与平面PBC所成二面角的余弦值.
,求平面PAD与平面PBC所成二面角的余弦值.
【答案】
(1)证明:依题: ![]() CD⊥面PADCD⊥AP,
CD⊥面PADCD⊥AP,
又AP⊥PD,∴AP⊥平面PCD,
又AP平面PAB,∴平面PAB⊥平面PCD;
(2)解:  AB∥CD
AB∥CD
由(1)知AB⊥面PAD∴ ![]() =
= ![]() ,
,
取AD中点O,PO⊥AD,平面PAD平面ABCD,∴PO平面ABCD,
以过点O且平行于AB的直线为x轴,如图建系,各点坐标如图.
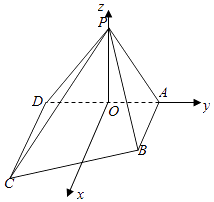
由(1)易知平面PAD的一法向量为 ![]() ,
,
设平面PBC的法向量为 ![]()
. ![]() ,
, ![]() .
. 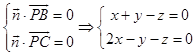 ,
,
取x=2, ![]() .
. ![]() =
= 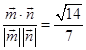 ,
,
故所求二面角的余弦值为 ![]() .
.
【解析】(1)依题意得CD⊥AP,AP⊥PD,即AP⊥平面PCD,可得平面PAB⊥平面PCD(2) ![]() ,AB∥CD
,AB∥CD
由(1)知AB⊥面PAD,由 ![]() =
= ![]() ,
,
取AD中点O,以过点O且平行于AB的直线为x轴建系,利用向量求解.
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知一个平面过另一个平面的垂线,则这两个平面垂直.


科目:高中数学 来源: 题型:
【题目】函数y=sin2x的图象经过适当变换可以得到y=cos2x的图象,则这种变换可以是( )
A.沿x轴向右平移 ![]() 个单位
个单位
B.沿x轴向左平移 ![]() 个单位
个单位
C.沿x轴向左平移 ![]() 个单位
个单位
D.沿x轴向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当n为正整数时,函数N(n)表示n的最大奇因数,如N(3)=3,N(10)=5,…,设Sn=N(1)+N(2)+N(3)+N(4)+…+N(2n﹣1)+N(2n),则Sn= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x﹣3y﹣6=0,点T(﹣1,1)在AD边所在直线上. (Ⅰ)求AD边所在直线的方程;
(Ⅱ)求矩形ABCD外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n=( )
A.9
B.10
C.12
D.13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m、n、s、t∈R* , m+n=3, ![]() 其中m、n是常数且m<n,若s+t的最小值 是
其中m、n是常数且m<n,若s+t的最小值 是 ![]() ,满足条件的点(m,n)是椭圆
,满足条件的点(m,n)是椭圆 ![]() 一弦的中点,则此弦所在的直线方程为( )
一弦的中点,则此弦所在的直线方程为( )
A.x﹣2y+3=0
B.4x﹣2y﹣3=0
C.x+y﹣3=0
D.2x+y﹣4=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com