Question

若函数y=f（x），如果存在给定的实数对（a，b），使得f（a+x）•f（a-x）=b恒成立，则称y=f（x）为“Ω函数”．
（1）判断下列函数，是否为“Ω函数”，并说明理由；
①f（x）=x³　　　　 ②f（x）=2^x
（2）已知函数f（x）=tanx是一个“Ω函数”，求出所有的有序实数对（a，b）．

Answer 1

解：（1）①若f（x）=x³ 是“Ω函数”，则存在实数对（a，b），使得f（a+x）•f（a-x）=b，
即（a²-x²）³=b时，对x∈R恒成立 …（2分）
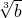
而x²=a²-最多有两个解，矛盾，
因此f（x）=x³ 不是“Ω函数”…（3分）
②若f（x）=2^x是“Ω函数”，则存在常数a，b使得2^a+x•2^a-x=2^2a，
即存在常数对（a，2^2a）满足，因此f（x）=2^x是“Ω函数”（6分）
（2）解：函数f（x）=tanx是一个“Ω函数”，
设有序实数对（a，b）满足，则tan（a-x）tan（a+x）=b恒成立
当a=kπ+，k∈Z时，tan（a-x）tan（a+x）=-cot²x，不是常数； 　…（8分）
因此a≠kπ+，k∈Z，当x≠mπ+，m∈Z时，
则有（btan²a-1）tan²x+（tan²a-b）=0恒成立，
所以btan²a-1=0且tan²a-b=0
∴tan²a=1，b=1
∴a=kπ+，k∈Z，b=1 　…（13分）
∴当x=mπ+，m∈Z，a=kπ±时，tan（a-x）tan（a+x）=cot²a=1．
因此满足f（x）=tanx是一个“Ω函数”的实数对（a，b）=（kπ±，1），k∈Z…（14分）
分析：（1）根据新定义，列出方程恒成立，通过判断方程的解的个数判断出f（x）=x³ 不是“Ω函数”，f（x）=2^x是“Ω函数”；
（2）据题中的定义，列出方程恒成立，通过两角和差的正切公式展开整理，令含未知数的系数为0，即可求出a，b．
点评：本题考查理解题中的新定义、判断函数是否具有特殊函数的条件、利用新定义得到恒等式、通过仿写的方法得到函数的递推关系，属于中档题．