
A. | B. | C. | D. |
科目:高中数学 来源:不详 题型:解答题
 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min. 的分布列及期望.
的分布列及期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
. 中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域
中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域 中的概率;
中的概率; 中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域
中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域 中的个数为
中的个数为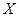 ,求
,求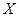 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (元)的概率分布列和期望
(元)的概率分布列和期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 2列联表:
2列联表:| | 会围棋 | 不会围棋 | 总计 |
| 男 | | | |
| 女 | | | |
| 总计 | | | 30 |
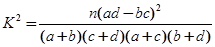 其中n=a+b+c+d
其中n=a+b+c+d | 0.40 | 0.25 | 0.10 | 0.010 |
 | 0.708 | 1.323 | 2.706 | 6.635 |
 ,求
,求 的期望.
的期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 局者获得这次比赛的胜利,比赛结束.假设在一局比赛中,甲获胜的概率为
局者获得这次比赛的胜利,比赛结束.假设在一局比赛中,甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为 ,各局比赛结果相互独立.现知前
,各局比赛结果相互独立.现知前 局中,甲、乙各胜
局中,甲、乙各胜 局,设
局,设 表示从第
表示从第 局开始到比赛结束所进行的局数,则
局开始到比赛结束所进行的局数,则 的数学期望为 .
的数学期望为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求 的分布列和数学期望
的分布列和数学期望 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com