
【题目】某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(如图(1))和女生身高情况的频率分布直方图(如图(2)).已知图(1)中身高在170~175cm的男生有16名.

(1)试问在抽取的学生中,男、女生各有多少名?
身高≥170cm | 身高<170cm | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)根据频率分布直方图,完成下面的2×2列联表,并判断能有多大(百分数)的把握认为身高与性别有关?
附:参考公式和临界值表
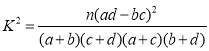
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1)男生40名,女生40名(2)见解析,能有99.9%的把握认为身高与性别有关.
【解析】
(1)由图(1)求出男生的人数为40,所以女生人数为40;
(2)完成列联表后,根据公式计算出![]() ,结合临界值表可得结论.
,结合临界值表可得结论.
解:(1)由题图(1)可知,身高在170~175 cm的男生的频率为0.08×5=0.4,设抽取的学生中,男生有n1名,则![]() ,解得n1=40.
,解得n1=40.
所以女生有80-40=40(名).
(2)由(1)及频率分布直方图知,身高≥170 cm的男生有(0.08+0.04+0.02+0.01)×5×40=30(名),身高≥170 cm的女生有0.02×5×40=4(名),所以可得下列列联表:
身高≥170cm | 身高<170cm | 总计 | |
男生 | 30 | 10 | 40 |
女生 | 4 | 36 | 40 |
总计 | 34 | 46 | 80 |
由列联表中数据得K2的观测值为![]() ≈34.578>10.828.
≈34.578>10.828.
所以能有99.9%的把握认为身高与性别有关.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,AB=2,BC=1,![]() ,E为PB中点.
,E为PB中点.
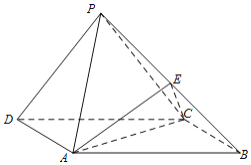
(Ⅰ)求证:PD∥平面ACE;
(Ⅱ)求证:PD⊥平面PBC;
(Ⅲ)求三棱锥E-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥P–ABC中,PA⊥平面ABC,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,则异面直线PC,AD所成角的余弦值为

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点F为抛物线C:![]() (
(![]() )的焦点,过点F的动直线l与抛物线C交于M,N两点,且当直线l的倾斜角为45°时,
)的焦点,过点F的动直线l与抛物线C交于M,N两点,且当直线l的倾斜角为45°时,![]() .
.

(1)求抛物线C的方程.
(2)试确定在x轴上是否存在点P,使得直线PM,PN关于x轴对称?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,以原点![]() 为圆心,
为圆心,![]()
![]() 为半径的定圆
为半径的定圆![]() ,与过原点且斜率为
,与过原点且斜率为![]()
![]() 的动直线交于
的动直线交于![]() 、
、![]() 两点,在
两点,在![]() 轴正半轴上有一个定点
轴正半轴上有一个定点![]() ,
,![]() 、
、![]() 、
、![]() 三点构成三角形,求:
三点构成三角形,求:
(1)△![]() 的面积
的面积![]() 的表达式,并求出
的表达式,并求出![]() 的取值范围;
的取值范围;
(2)△![]() 的外接圆
的外接圆![]() 的面积
的面积![]() 的表达式,并求出
的表达式,并求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】继空气净化器之后,某商品成为人们抗雾霾的有力手段,根据该商品厂提供的数据,从2015年到2018年,购买该商品的人数直线上升,根据统计图, 说法错误的是( )

A. 连续3年,该商品在1月的销售量增长显著。
B. 2017年11月到2018年2月销量最多。
C. 从统计图上可以看出,2017年该商品总销量不超过6000台。
D. 2018年2月比2017年2月该商品总销量少。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为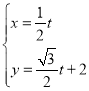 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求直线![]() 被曲线
被曲线![]() 所截得的弦长.
所截得的弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com