
【题目】某大型运动会的组委会为了搞好接待工作,招募了30名男志愿者和20名女志愿者.调查发现,这些志愿者中有部分志愿者喜爱运动,另一部分志愿者不喜欢运动,并得到了如下等高条形图和![]() 列联表:
列联表:
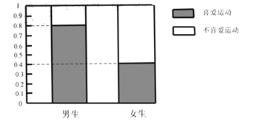
喜爱运动 | 不喜爱运动 | 总计 | |
男生 |
|
| 30 |
女生 |
|
| 20 |
总计 | 50 |
(1)求出列联表中![]()
![]()
![]()
![]() 的值;
的值;
(2)是否有![]() 的把握认为喜爱运动与性别有关?附:参考公式和数据:
的把握认为喜爱运动与性别有关?附:参考公式和数据: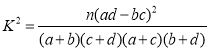 ,(其中
,(其中![]() )
)
0.500 | 0.100 | 0.050 | 0.010 | 0.001 | |
| 0.455 | 2.706 | 3.841 | 6.635 | 10.828 |
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 是直线
是直线![]() 上的动点,
上的动点,![]() 为定点,点
为定点,点![]() 为
为![]() 的中点,动点
的中点,动点![]() 满足
满足![]() ,且
,且![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线交曲线
的直线交曲线![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为曲线
为曲线![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点.问
两点.问![]() 是否为定值?若是,求
是否为定值?若是,求![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】迈入2018年后,直播答题突然就火了.在1月6号的一场活动中,最终仅有23人平分100万,这23人可以说是“学霸”级的大神.随着直播答题的发展,平台“烧钱大战”模式的可持续性受到了质疑,某网站随机选取1000名网民进行了调查,得到的数据如下表:
男 | 女 | |
认为直播答题模式可持续 | 360 | 280 |
认为直播答题模式不可持续 | 240 | 120 |
(1)根据表格中的数据,能否在犯错误不超过![]() 的前提下,认为对直播答题模式的态度与性别有关系?
的前提下,认为对直播答题模式的态度与性别有关系?
(2)已知在参与调查的1000人中,有20%曾参加答题游戏瓜分过奖金,而男性被调查者有15%曾参加游戏瓜分过奖金,求女性被调查者参与游戏瓜分过奖金的概率.
参考公式: ![]() .
.
临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.2018年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本2500万元,每生产x(百辆),需另投入成本![]() 万元,且
万元,且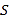 .由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
.由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
(1)求出2018年的利润L(x)(万元)关于年产量x(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,点
为坐标原点,点![]() ,
,![]() ,
,![]() ,动点
,动点![]() 满足
满足![]() ,点
,点![]() 为线段
为线段![]() 的中点,抛物线
的中点,抛物线![]() :
:![]() 上点
上点![]() 的纵坐标为
的纵坐标为![]() ,
,![]() .
.
(1)求动点![]() 的轨迹曲线
的轨迹曲线![]() 的标准方程及抛物线
的标准方程及抛物线![]() 的标准方程;
的标准方程;
(2)若抛物线![]() 的准线上一点
的准线上一点![]() 满足
满足![]() ,试判断
,试判断![]() 是否为定值,若是,求这个定值;若不是,请说明理由.
是否为定值,若是,求这个定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com