
分析 (1)通过an=3Sn-2与an-1=3Sn-1-2(n≥2)作差、整理可知an=-$\frac{1}{2}$an-1(n≥2),进而可知数列{an}是首项为1、公比为-$\frac{1}{2}$的等比数列,计算即得结论;
(2)通过(1)可知nan=(-1)n-1•$\frac{n}{{2}^{n-1}}$,进而利用错位相减法计算即得结论.
解答 解:(1)∵an=3Sn-2,
∴an-1=3Sn-1-2(n≥2),
两式相减得:an-an-1=3an,
整理得:an=-$\frac{1}{2}$an-1(n≥2),
又∵a1=3S1-2,即a1=1,
∴数列{an}是首项为1、公比为-$\frac{1}{2}$的等比数列,
∴其通项公式an=(-1)n-1•$\frac{1}{{2}^{n-1}}$;
(2)由(1)可知nan=(-1)n-1•$\frac{n}{{2}^{n-1}}$,
∴Tn=1•1+(-1)•2•$\frac{1}{2}$+…+(-1)n-2•(n-1)•$\frac{1}{{2}^{n-2}}$+(-1)n-1•$\frac{n}{{2}^{n-1}}$,
∴-$\frac{1}{2}$Tn=1•(-1)•$\frac{1}{2}$+2•$\frac{1}{{2}^{2}}$+…+(-1)n-1•(n-1)•$\frac{1}{{2}^{n-1}}$+(-1)n•n•$\frac{1}{{2}^{n}}$,
错位相减得:$\frac{3}{2}$Tn=1+[-$\frac{1}{2}$+$\frac{1}{{2}^{2}}$-$\frac{1}{{2}^{3}}$+…+(-1)n-1•$\frac{1}{{2}^{n-1}}$]-(-1)n•n•$\frac{1}{{2}^{n}}$
=1+$\frac{-\frac{1}{2}[1-(-1)^{n-1}•\frac{1}{{2}^{n-1}}]}{1-(-\frac{1}{2})}$-(-1)n•n•$\frac{1}{{2}^{n}}$
=$\frac{2}{3}$+(-1)n-1•$\frac{3n+2}{3}$•$\frac{1}{{2}^{n}}$,
∴Tn=$\frac{2}{3}$[$\frac{2}{3}$+(-1)n-1•$\frac{3n+2}{3}$•$\frac{1}{{2}^{n}}$]=$\frac{4}{9}$+(-1)n-1•$\frac{3n+2}{9}$•$\frac{1}{{2}^{n-1}}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
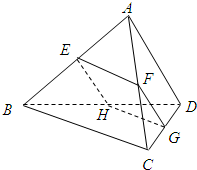 如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是$\frac{1}{4}{a}^{2}$.
如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是$\frac{1}{4}{a}^{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,E为SC的中点,SD=AD.
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,E为SC的中点,SD=AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一个空间几何体的三视图如图所示,其中正视图与左视图上方均为等边三角形,根据图中数据:
一个空间几何体的三视图如图所示,其中正视图与左视图上方均为等边三角形,根据图中数据:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com