分析:(1)连接BO,取DO中点H,连接GH,由题意可得:平面AD1⊥平面AC,进而证明BO⊥平面AD1,由GH与OB的关系可得答案.
(2)建立空间直角坐标系,根据题意分别求出两个平面的法向量,结合向量间的运算关系求出两个向量的夹角.进而转化为二面角的平面角.
解答:
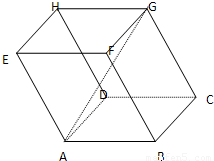
解:(1)连接BO,取DO中点H,连接GH,
因为A
1O⊥平面AC,所以平面AD
1⊥平面AC,
又底面为菱形,O为AD中点,
所以BO⊥平面AD
1,
因为GH∥BO,
所以GH⊥平面AD
1,
又GH=
BD=
,
所以点G到平面ADD
1A
1的距离为
.
(2)分别以OA,OB,OA
1所在直线为x,y,z轴,建立如图所示的坐标系,
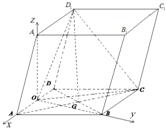
则
G(-,,0),D
1(-2,0,a),所以
=(,,-a),
面AD
1的一个法向量
n=(0,,0),
所以
cos?n,>==,解得a=1,
因为面OCD的一个法向量为n=(0,0,1),
设面OCD
1的一个法向量为p=(x,y,z),则
=(-2,0,1),
=(-2,,0),
则有
所以
,
取
x=,
m=(,2,2),
则
cos<p,m>==,
所以二面角D-OC-D
1的大小为
arccos.
点评:夹角成立问题的关键是数列掌握几何体的结构特征,以便得到线面关系以及建立坐标系,利用向量夹角空间角,空间距离等问题.

 如图,平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的菱形,∠BAD=
如图,平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的菱形,∠BAD= 解:(1)连接BO,取DO中点H,连接GH,
解:(1)连接BO,取DO中点H,连接GH, 则 G(-
则 G(-

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案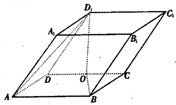 如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.
如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.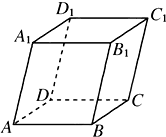 如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,