
已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证:(1)△ABC≌△DCB
(2)DE·DC=AE·BD.
(1)根据梯形为等腰梯形推断出∠ABC=∠DCB,同时根据AB=CD,BC=CB,证明出△ABC≌△DCB.
(2)根据(1)中△ABC≌△DCB推断出∠ACB=∠DBC,同时根据AD∥BC和ED∥AC推断出∠EDA=∠DBC,∠EAD=∠DCB,进而根据相似三角形判定定理推断出△ADE∽△CBD,进而根据相似三角形的性质求得DE:BD=AE:CD,推断出DE?DC=AE?BD.
【解析】
试题分析:证明:(1) ∵四边形ABCD是等腰梯形,∴AC=DB
∵AB=DC,BC=CB,∴△ABC≌△BCD
(2)∵△ABC≌△BCD,∴∠ACB=∠DBC,∠ABC=∠DCB
∵AD∥BC,∴∠DAC=∠ACB,∠EAD=∠ABC
∵ED∥AC,∴∠EDA=∠DAC ∴∠EDA=∠DBC,∠EAD=∠DCB
∴△ADE∽△CBD ∴DE:BD=AE:CD, ∴DE·DC=AE·BD.
考点:相似三角形
点评:本题主要考查了相似三角形的判定.考查了学生对基础知识的熟练掌握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,已知椭圆G:
如图,已知椭圆G:| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:2011年湖南省高二数学选修4-1《几何证明选讲》单元练习题 题型:解答题
已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证:(1)△ABC≌△DCB (2)DE·DC=AE·BD.
查看答案和解析>>
科目:高中数学 来源:2013届度辽宁省高二12月月考数学试题 题型:解答题
已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证:(1)△ABC≌△DCB (2)DE·DC=AE·BD.

查看答案和解析>>
科目:高中数学 来源:2010年新疆农七师高级中学高二第二学期第二阶段考试数学(文)试题 题型:解答题
(本小题满分12分)已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.
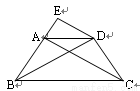
求证:(1)△ABC≌△DCB
(2)DE·DC=AE·BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com