
【题目】在平面直角坐标系中,正三角形ABC的边BC所在直线斜率是0,则AC、AB所在的直线斜率之和为( )
A.- ![]()
B.0
C.![]()
D.![]()
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱柱ABC﹣A1B1C1的,底面边长是侧棱长2倍,D、E是A1C1、AC的中点,则下面判断不正确的为( ) 
A.直线A1E∥平面B1DC
B.直线AD⊥平面B1DC
C.平面B1DC⊥平面ACC1A1
D.直线AC与平面B1DC所成的角为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(Ⅰ)完成被调查人员的频率分布直方图;

(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率;

(Ⅲ)在(Ⅱ)的条件下,再记选中的4人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线方程为x2=2py(p>0),其焦点为F,点O为坐标原点,过焦点F作斜率为k(k≠0)的直线与抛物线交于A,B两点,过A,B两点分别作抛物线的两条切线,设两条切线交于点M.
(1)求 ![]() ;
;
(2)设直线MF与抛物线交于C,D两点,且四边形ACBD的面积为 ![]() ,求直线AB的斜率k.
,求直线AB的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,点P是CD上的动点,则直线B1P与直线BC1所成的角等于( ) 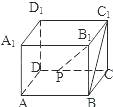
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】ABCD为正方形,P为平面ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC,平面PAB与平面PAD的位置关系是( )
A.平面PAB与平面PAD,PBC垂直
B.它们都分别相交且互相垂直
C.平面PAB与平面PAD垂直,与平面PBC相交但不垂直
D.平面PAB与平面PBC垂直,与平面PAD相交但不垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合U={x∈N|0<x≤8},S={1,2,4,5},T={3,5,7},则S∩(CUT)=( )
A.{1,2,4}
B.{1,2,3,4,5,7}
C.{1,2}
D.{1,2,4,5,6,8}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com